Python pour la data science

Lino Galiana

doi:10.5281/zenodo.8229676

path = window.location.pathname.replace(".html", ".qmd");
path_modified = (path.includes('en/content')) ? path.replace('en/content', 'content/en') : path
html`${printBadges({fpath: path_modified})}`

html`<div>${getConditionalHTML(path, true)}</div>`

function isBetweenSeptAndDec() {
    const now = new Date();
    const start = new Date(now.getFullYear(), 8, 1); // September 1st (month is zero-indexed)
    const end = new Date(now.getFullYear(), 11, 24); // December 24th (month is zero-indexed)
    
    return now >= start && now <= end;
}

function getConditionalHTML(path, print) {
    if (print === false) return ``
    if (isBetweenSeptAndDec()) {
        return md`<i>La correction sera visible prochainement sur cette page. En attendant, la liste des corrections déjà acccessibles est [ici](/content/annexes/corrections.html)</i>`; // Return an empty string if not between the dates
    } else {
        return html`
        <details>
            <summary>
                Pour ouvrir la version corrigée sous forme de <i>notebook</i>
            </summary>
            ${printBadges({ fpath: path, correction: true })}
        </details>
        `;
    }
}

function renderCorrection({ fpath, correction }) {
    if (correction) {
        return html`${printBadges({ fpath: fpath, correction: true })}`;
    } else {
        return html`<i>La correction sera visible prochainement sur cette page.</i>`;
    }
}

function reminderBadges({
    sourceFile = "content/01_toto.Rmd",
    type = ['md', 'html'],
    split = null,
    onyxiaOnly = false,
    sspCloudService = "python",
    GPU = false,
    correction = false
} = {}) {
    if (Array.isArray(type)) {
        type = type[0];
    }

    let notebook = sourceFile.replace(/(.Rmd|.qmd)/, ".ipynb");
    if (correction) {
        notebook = notebook.replace(/content/, "corrections");
    } else {
        notebook = notebook.replace(/content/, "notebooks");
    }

    const githubRepoNotebooksSimplified = "github/linogaliana/python-datascientist-notebooks";
    const githubAlias = githubRepoNotebooksSimplified.replace("github", "github.com");
    const githubRepoNotebooks = `https://${githubAlias}`;

    let githubLink ;

    if (notebook === "") {
        githubLink = githubRepoNotebooks;
    } else {
        githubLink = `${githubRepoNotebooks}/blob/main`;
    }

    const notebookRelPath = `/${notebook}`;
    const [section, chapter] = notebook.split("/").slice(-2);

    githubLink = `<a href="${githubLink}${notebookRelPath}" class="github"><i class="fab fa-github"></i></a>`;

    let sectionLatest = section.split("/").slice(-1)[0];
    const chapterNoExtension = chapter.replace(".ipynb", "");
    
    if (sourceFile.includes('en/')) {
        sectionLatest = `en/${sectionLatest}`;
    }

    const onyxiaInitArgs = [sectionLatest, chapterNoExtension];

    if (correction) {
        onyxiaInitArgs.push("correction");
    }

    const gpuSuffix = GPU ? "-gpu" : "";

    const sspcloudJupyterLinkLauncher = `https://datalab.sspcloud.fr/launcher/ide/jupyter-${sspCloudService}${gpuSuffix}?autoLaunch=true&onyxia.friendlyName=%C2%AB${chapterNoExtension}%C2%BB&init.personalInit=%C2%ABhttps%3A%2F%2Fraw.githubusercontent.com%2Flinogaliana%2Fpython-datascientist%2Fmaster%2Fsspcloud%2Finit-jupyter.sh%C2%BB&init.personalInitArgs=%C2%AB${onyxiaInitArgs.join('%20')}%C2%BB`;

    let sspcloudJupyterLink;
    if (type === "md") {
        sspcloudJupyterLink = `[![Onyxia](https://img.shields.io/badge/SSP%20Cloud-Lancer_avec_Jupyter-orange?logo=Jupyter&logoColor=orange)](${sspcloudJupyterLinkLauncher})`;
    } else {
        sspcloudJupyterLink = `<a href="${sspcloudJupyterLinkLauncher}" target="_blank" rel="noopener"><img src="https://img.shields.io/badge/SSP%20Cloud-Lancer_avec_Jupyter-orange?logo=Jupyter&logoColor=orange" alt="Onyxia"></a>`;
    }

    if (split === 4) {
        sspcloudJupyterLink += '<br>';
    }

    const sspcloudVscodeLinkLauncher = `https://datalab.sspcloud.fr/launcher/ide/vscode-${sspCloudService}${gpuSuffix}?autoLaunch=true&onyxia.friendlyName=%C2%AB${chapterNoExtension}%C2%BB&init.personalInit=%C2%ABhttps%3A%2F%2Fraw.githubusercontent.com%2Flinogaliana%2Fpython-datascientist%2Fmaster%2Fsspcloud%2Finit-vscode.sh%C2%BB&init.personalInitArgs=%C2%AB${onyxiaInitArgs.join('%20')}%C2%BB`;

    let sspcloudVscodeLink;
    if (type === "md") {
        sspcloudVscodeLink = `[![Onyxia](https://img.shields.io/badge/SSP%20Cloud-Lancer_avec_VSCode-blue?logo=visualstudiocode&logoColor=blue)](${sspcloudVscodeLinkLauncher})`;
    } else {
        sspcloudVscodeLink = `<a href="${sspcloudVscodeLinkLauncher}" target="_blank" rel="noopener"><img src="https://img.shields.io/badge/SSP%20Cloud-Lancer_avec_VSCode-blue?logo=visualstudiocode&logoColor=blue" alt="Onyxia"></a>`;
    }

    if (split === 5) {
        sspcloudVscodeLink += '<br>';
    }

    let colabLink;
    if (type === "md") {
        colabLink = `[![Open In Colab](https://colab.research.google.com/assets/colab-badge.svg)](http://colab.research.google.com/${githubRepoNotebooksSimplified}/blob/main${notebookRelPath})`;
    } else {
        colabLink = `<a href="https://colab.research.google.com/${githubRepoNotebooksSimplified}/blob/main${notebookRelPath}" target="_blank" rel="noopener"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"></a>`;
    }

    if (split === 7) {
        colabLink += '<br>';
    }

    let vscodeLink;
    if (type === "md") {
        vscodeLink = `[![githubdev](https://img.shields.io/static/v1?logo=visualstudiocode&label=&message=Open%20in%20Visual Studio Code&labelColor=2c2c32&color=007acc&logoColor=007acc)](https://github.dev/linogaliana/python-datascientist-notebooks${notebookRelPath})`;
    } else {
        vscodeLink = `<a href="https://github.dev/linogaliana/python-datascientist-notebooks${notebookRelPath}" target="_blank" rel="noopener"><img src="https://img.shields.io/static/v1?logo=visualstudiocode&label=&message=Open%20in%20Visual%20Studio%20Code&labelColor=2c2c32&color=007acc&logoColor=007acc" alt="githubdev"></a></p>`;
    }

    const badges = [
        githubLink,
        sspcloudVscodeLink,
        sspcloudJupyterLink
    ];

    if (!onyxiaOnly) {
        badges.push(colabLink);
    }

    let result = badges.join("\n");

    if (type === "html") {
        result = `<p class="badges">${result}</p>`;
    }

    if (onyxiaOnly) {
        result = `${sspcloudJupyterLink}${sspcloudVscodeLink}`;
    }

    return result;
}


function printBadges({
    fpath,
    onyxiaOnly = false,
    split = 5,
    type = "html",
    sspCloudService = "python",
    GPU = false,
    correction = false
} = {}) {
    const badges = reminderBadges({
        sourceFile: fpath,
        type: type,
        split: split,
        onyxiaOnly: onyxiaOnly,
        sspCloudService: sspCloudService,
        GPU: GPU,
        correction: correction
    });

    return badges
}

Ce chapitre utilise toujours le même jeu de données, présenté dans l’introduction de cette partie : les données de vote aux élections présidentielles américaines croisées à des variables sociodémographiques. Le code est disponible sur Github.

!pip install --upgrade xlrd #colab bug verson xlrd
!pip install geopandas

import requests

url = "https://raw.githubusercontent.com/linogaliana/python-datascientist/main/content/modelisation/get_data.py"
r = requests.get(url, allow_redirects=True)
open("getdata.py", "wb").write(r.content)

import getdata

votes = getdata.create_votes_dataframes()

Pour ce TP, nous aurons besoin des packages suivants :

import pandas as pd
import matplotlib.pyplot as plt

0.1 La méthode des SVM (Support Vector Machines)

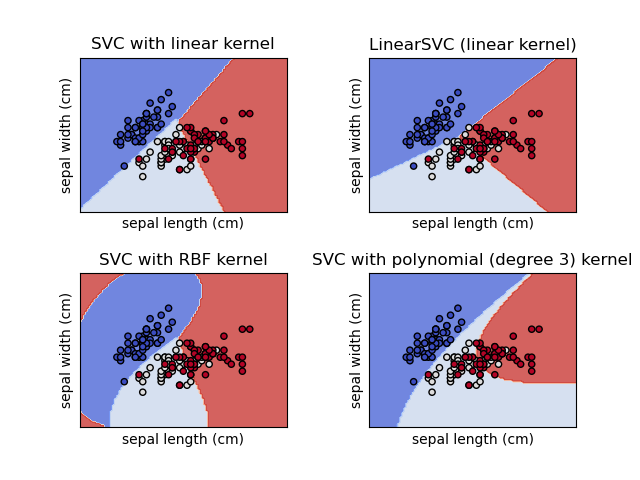
L’une des méthodes de machine learning les plus utilisées en classification sont les SVM (Support Vector Machines). Il s’agit de trouver, dans un système de projection adéquat (noyau ou kernel), les paramètres de l’hyperplan (en fait d’un hyperplan à marges maximales) séparant les classes de données :

Formalisation mathématique

Les SVM sont l’une des méthodes de machine learning les plus intuitives du fait de l’interprétation géométrique simple de la méthode. Il s’agit aussi d’un des algorithmes de machine learning à la formalisation la moins complexe pour les praticiens ayant des notions en statistique traditionnelle. Cette boîte revient dessus. Néanmoins, celle-ci n’est pas nécessaire à la compréhension du chapitre. En machine learning, plus que les détails mathématiques, l’important est d’avoir des intuitions.

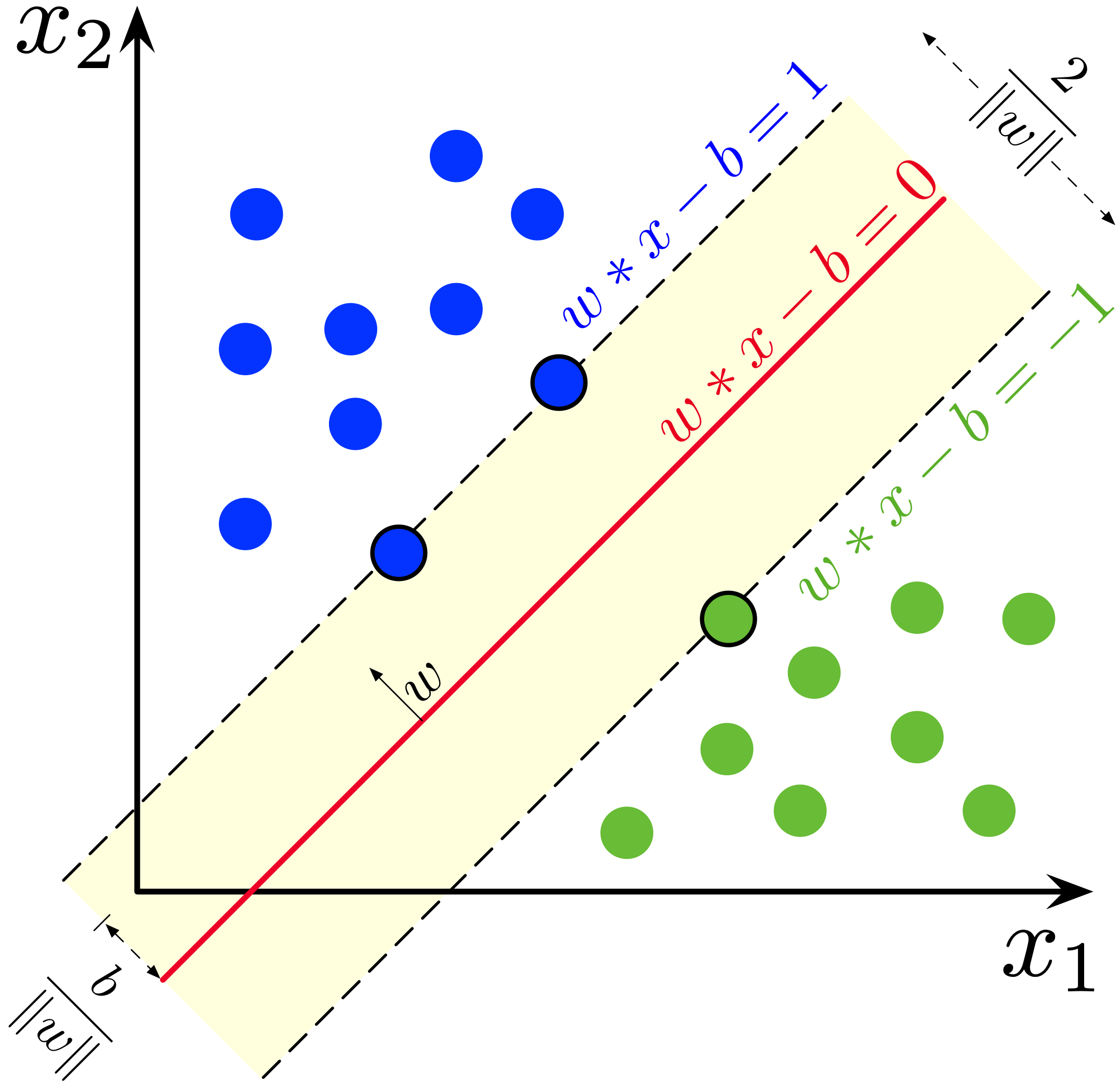
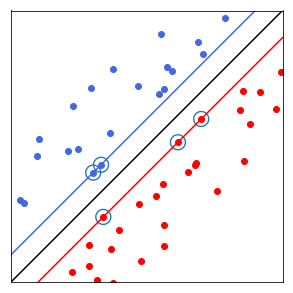
L’objectif des SVM est, rappelons-le, de trouver un hyperplan qui permette de séparer les différentes classes au mieux. Par exemple, dans un espace à deux dimensions, il s’agit de trouver une droite avec des marges qui permette de séparer au mieux l’espace en partie avec des labels homogènes.

On peut, sans perdre de généralité, supposer que le problème consiste à supposer l’existence d’une loi de probabilité \(\mathbb{P}(x,y)\) (\(\mathbb{P} \to \{-1,1\}\)) qui est inconnue. Le problème de discrimination vise à construire un estimateur de la fonction de décision idéale qui minimise la probabilité d’erreur, autrement dit

\[ \theta = \arg\min_\Theta \mathbb{P}(h_\theta(X) \neq y |x) \]

Les SVM les plus simples sont les SVM linéaires. Dans ce cas, on suppose qu’il existe un séparateur linéaire qui permet d’associer chaque classe à son signe:

\[ h_\theta(x) = \text{signe}(f_\theta(x)) ; \text{ avec } f_\theta(x) = \theta^T x + b \] avec \(\theta \in \mathbb{R}^p\) et \(w \in \mathbb{R}\).

Lorsque des observations sont linéairement séparables, il existe une infinité de frontières de décision linéaire séparant les deux classes. Le “meilleur” choix est de prendre la marge maximale permettant de séparer les données. La distance entre les deux marges est \(\frac{2}{||\theta||}\). Donc maximiser cette distance entre deux hyperplans revient à minimiser \(||\theta||^2\) sous la contrainte \(y_i(\theta^Tx_i + b) \geq 1\).

Dans le cas non linéairement séparable, la hinge loss \(\max\big(0,y_i(\theta^Tx_i + b)\big)\) permet de linéariser la fonction de perte:

ce qui donne le programme d’optimisation suivant :

\[ \frac{1}{n} \sum_{i=1}^n \max\big(0,y_i(\theta^Tx_i + b)\big) + \lambda ||\theta||^2 \]

La généralisation au cas non linéaire implique d’introduire des noyaux transformant l’espace de coordonnées des observations.

0.2 Application

Pour appliquer un modèle de classification, il nous faut trouver une variable dichotomique. Le choix naturel est de prendre la variable dichotomique qu’est la victoire ou défaite d’un des partis.

Même si les Républicains ont perdu en 2020, ils l’ont emporté dans plus de comtés (moins peuplés). Nous allons considérer que la victoire des Républicains est notre label 1 et la défaite 0.

Exercice 1 : Premier algorithme de classification

Créer une variable dummy appelée y dont la valeur vaut 1 quand les républicains l’emportent.
En utilisant la fonction prête à l’emploi nommée train_test_split de la librairie sklearn.model_selection, créer des échantillons de test (20 % des observations) et d’estimation (80 %) avec comme features : 'Unemployment_rate_2019', 'Median_Household_Income_2019', 'Percent of adults with less than a high school diploma, 2015-19', "Percent of adults with a bachelor's degree or higher, 2015-19" et comme label la variable y.

Note: Il se peut que vous ayez le warning suivant :

A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel()

Note : Pour éviter ce warning à chaque fois que vous estimez votre modèle, vous pouvez utiliser DataFrame[['y']].values.ravel() plutôt que DataFrame[['y']] lorsque vous constituez vos échantillons.

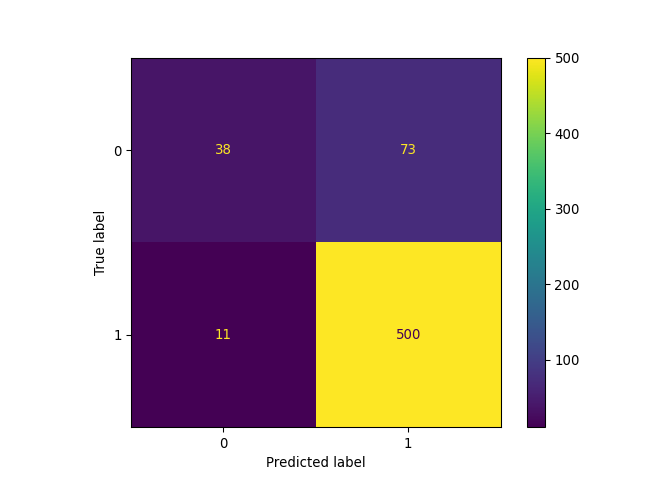
Entraîner un classifieur SVM avec comme paramètre de régularisation C = 1. Regarder les mesures de performance suivante : accuracy, f1, recall et precision.
Vérifier la matrice de confusion : vous devriez voir que malgré des scores en apparence pas si mauvais, il y a un problème notable.
Refaire les questions précédentes avec des variables normalisées. Le résultat est-il différent ?
Changer de variables x. Utiliser uniquement le résultat passé du vote démocrate (année 2016) et le revenu. Les variables en question sont share_2016_republican et Median_Household_Income_2019. Regarder les résultats, notamment la matrice de confusion.
[OPTIONNEL] Faire une 5-fold validation croisée pour déterminer le paramètre C idéal.

A l’issue de la question 3, le classifieur avec C = 1 devrait avoir les performances suivantes :

	Score
Accuracy	0.882637
Recall	0.897297
Precision	0.968872
F1	0.931712

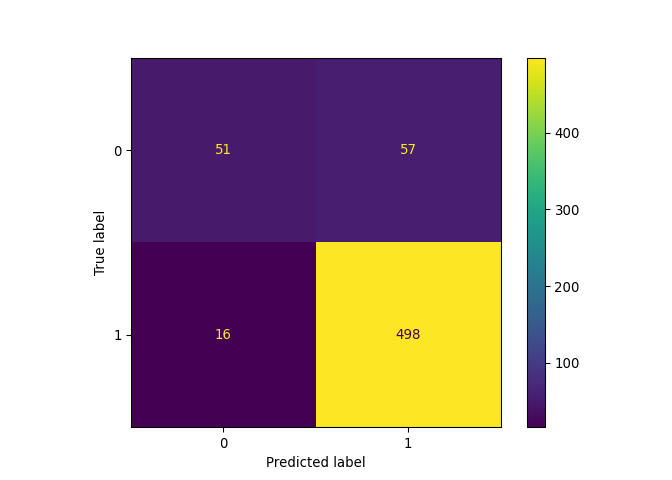
La matrice de confusion associée prend cette forme:

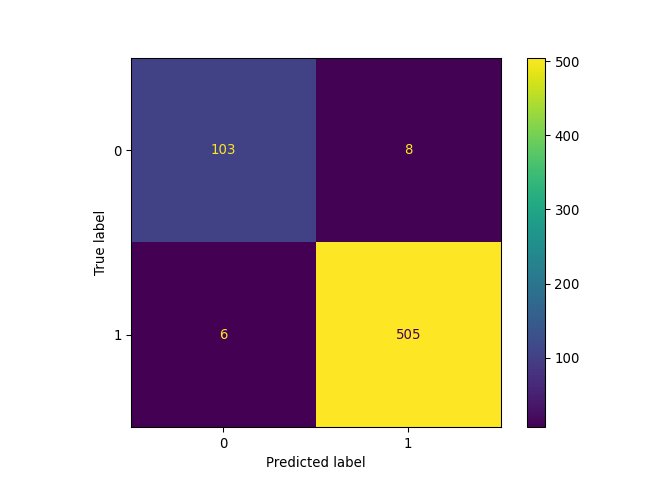
A l’issue de la question 6, le nouveau classifieur avec devrait avoir les performances suivantes :

	Score
Accuracy	0.882637
Recall	0.897297
Precision	0.968872
F1	0.931712

Et la matrice de confusion associée :

Informations additionnelles

environment files have been tested on.

Latest built version: 2024-11-20

Python version used:

'3.12.6 | packaged by conda-forge | (main, Sep 30 2024, 18:08:52) [GCC 13.3.0]'

Package	Version
affine	2.4.0
aiobotocore	2.15.1
aiohappyeyeballs	2.4.3
aiohttp	3.10.8
aioitertools	0.12.0
aiosignal	1.3.1
alembic	1.13.3
altair	5.4.1
aniso8601	9.0.1
annotated-types	0.7.0
appdirs	1.4.4
archspec	0.2.3
asttokens	2.4.1
attrs	24.2.0
babel	2.16.0
bcrypt	4.2.0
beautifulsoup4	4.12.3
black	24.8.0
blinker	1.8.2
blis	0.7.11
bokeh	3.5.2
boltons	24.0.0
boto3	1.35.23
botocore	1.35.23
branca	0.7.2
Brotli	1.1.0
cachetools	5.5.0
cartiflette	0.0.2
Cartopy	0.24.1
catalogue	2.0.10
cattrs	24.1.2
certifi	2024.8.30
cffi	1.17.1
charset-normalizer	3.3.2
click	8.1.7
click-plugins	1.1.1
cligj	0.7.2
cloudpathlib	0.20.0
cloudpickle	3.0.0
colorama	0.4.6
comm	0.2.2
commonmark	0.9.1
conda	24.9.1
conda-libmamba-solver	24.7.0
conda-package-handling	2.3.0
conda_package_streaming	0.10.0
confection	0.1.5
contextily	1.6.2
contourpy	1.3.0
cryptography	43.0.1
cycler	0.12.1
cymem	2.0.8
cytoolz	1.0.0
dask	2024.9.1
dask-expr	1.1.15
databricks-sdk	0.33.0
debugpy	1.8.6
decorator	5.1.1
Deprecated	1.2.14
diskcache	5.6.3
distributed	2024.9.1
distro	1.9.0
docker	7.1.0
duckdb	0.10.1
en-core-web-sm	3.7.1
entrypoints	0.4
et_xmlfile	2.0.0
exceptiongroup	1.2.2
executing	2.1.0
fastexcel	0.11.6
fastjsonschema	2.20.0
fiona	1.10.1
Flask	3.0.3
folium	0.17.0
fontawesomefree	6.6.0
fonttools	4.54.1
frozendict	2.4.4
frozenlist	1.4.1
fsspec	2023.12.2
funcy	2.0
gensim	4.3.2
geographiclib	2.0
geopandas	1.0.1
geoplot	0.5.1
geopy	2.4.1
gitdb	4.0.11
GitPython	3.1.43
google-auth	2.35.0
graphene	3.3
graphql-core	3.2.4
graphql-relay	3.2.0
graphviz	0.20.3
great-tables	0.12.0
greenlet	3.1.1
gunicorn	22.0.0
h2	4.1.0
hpack	4.0.0
htmltools	0.6.0
hyperframe	6.0.1
idna	3.10
imageio	2.36.0
importlib_metadata	8.5.0
importlib_resources	6.4.5
inflate64	1.0.0
ipykernel	6.29.5
ipython	8.28.0
itsdangerous	2.2.0
jedi	0.19.1
Jinja2	3.1.4
jmespath	1.0.1
joblib	1.4.2
jsonpatch	1.33
jsonpointer	3.0.0
jsonschema	4.23.0
jsonschema-specifications	2024.10.1
jupyter-cache	1.0.0
jupyter_client	8.6.3
jupyter_core	5.7.2
kaleido	0.2.1
kiwisolver	1.4.7
langcodes	3.5.0
language_data	1.3.0
lazy_loader	0.4
libmambapy	1.5.9
locket	1.0.0
lxml	5.3.0
lz4	4.3.3
Mako	1.3.5
mamba	1.5.9
mapclassify	2.8.1
marisa-trie	1.2.1
Markdown	3.6
markdown-it-py	3.0.0
MarkupSafe	2.1.5
matplotlib	3.9.2
matplotlib-inline	0.1.7
mdurl	0.1.2
menuinst	2.1.2
mercantile	1.2.1
mizani	0.11.4
mlflow	2.16.2
mlflow-skinny	2.16.2
msgpack	1.1.0
multidict	6.1.0
multivolumefile	0.2.3
munkres	1.1.4
murmurhash	1.0.10
mypy-extensions	1.0.0
narwhals	1.14.1
nbclient	0.10.0
nbformat	5.10.4
nest_asyncio	1.6.0
networkx	3.3
nltk	3.9.1
numexpr	2.10.1
numpy	1.26.4
opencv-python-headless	4.10.0.84
openpyxl	3.1.5
opentelemetry-api	1.16.0
opentelemetry-sdk	1.16.0
opentelemetry-semantic-conventions	0.37b0
OWSLib	0.28.1
packaging	24.1
pandas	2.2.3
paramiko	3.5.0
parso	0.8.4
partd	1.4.2
pathspec	0.12.1
patsy	0.5.6
Pebble	5.0.7
pexpect	4.9.0
pickleshare	0.7.5
pillow	10.4.0
pip	24.2
platformdirs	4.3.6
plotly	5.24.1
plotnine	0.13.6
pluggy	1.5.0
polars	1.8.2
preshed	3.0.9
prometheus_client	0.21.0
prometheus_flask_exporter	0.23.1
prompt_toolkit	3.0.48
protobuf	4.25.3
psutil	6.0.0
ptyprocess	0.7.0
pure_eval	0.2.3
py7zr	0.20.8
pyarrow	17.0.0
pyarrow-hotfix	0.6
pyasn1	0.6.1
pyasn1_modules	0.4.1
pybcj	1.0.2
pycosat	0.6.6
pycparser	2.22
pycryptodomex	3.21.0
pydantic	2.9.2
pydantic_core	2.23.4
Pygments	2.18.0
pyLDAvis	3.4.1
PyNaCl	1.5.0
pynsee	0.1.8
pyogrio	0.10.0
pyOpenSSL	24.2.1
pyparsing	3.1.4
pyppmd	1.1.0
pyproj	3.7.0
pyshp	2.3.1
PySocks	1.7.1
python-dateutil	2.9.0
python-dotenv	1.0.1
python-magic	0.4.27
pytz	2024.1
pyu2f	0.1.5
pywaffle	1.1.1
PyYAML	6.0.2
pyzmq	26.2.0
pyzstd	0.16.2
querystring_parser	1.2.4
rasterio	1.4.2
referencing	0.35.1
regex	2024.9.11
requests	2.32.3
requests-cache	1.2.1
retrying	1.3.4
rich	13.9.4
rpds-py	0.21.0
rsa	4.9
ruamel.yaml	0.18.6
ruamel.yaml.clib	0.2.8
s3fs	2023.12.2
s3transfer	0.10.2
scikit-image	0.24.0
scikit-learn	1.5.2
scipy	1.13.0
seaborn	0.13.2
setuptools	74.1.2
shapely	2.0.6
shellingham	1.5.4
six	1.16.0
smart-open	7.0.5
smmap	5.0.0
sortedcontainers	2.4.0
soupsieve	2.5
spacy	3.7.5
spacy-legacy	3.0.12
spacy-loggers	1.0.5
SQLAlchemy	2.0.35
sqlparse	0.5.1
srsly	2.4.8
stack-data	0.6.2
statsmodels	0.14.4
tabulate	0.9.0
tblib	3.0.0
tenacity	9.0.0
texttable	1.7.0
thinc	8.2.5
threadpoolctl	3.5.0
tifffile	2024.9.20
toolz	1.0.0
topojson	1.9
tornado	6.4.1
tqdm	4.66.5
traitlets	5.14.3
truststore	0.9.2
typer	0.13.1
typing_extensions	4.12.2
tzdata	2024.2
Unidecode	1.3.8
url-normalize	1.4.3
urllib3	1.26.20
wasabi	1.1.3
wcwidth	0.2.13
weasel	0.4.1
webdriver-manager	4.0.2
websocket-client	1.8.0
Werkzeug	3.0.4
wheel	0.44.0
wordcloud	1.9.3
wrapt	1.16.0
xgboost	2.1.1
xlrd	2.0.1
xyzservices	2024.9.0
yarl	1.13.1
yellowbrick	1.5
zict	3.0.0
zipp	3.20.2
zstandard	0.23.0

View file history

md`Ce fichier a été modifié __${table_commit.length}__ fois depuis sa création le ${creation_string} (dernière modification le ${last_modification_string})`

creation = d3.min(
  table_commit.map(d => new Date(d.Date))
)

last_modification = d3.max(
  table_commit.map(d => new Date(d.Date))
)

creation_string = creation.toLocaleString("fr", {
  "day": "numeric",
  "month": "long",
  "year": "numeric"
})

last_modification_string = last_modification.toLocaleString("fr", {
  "day": "numeric",
  "month": "long",
  "year": "numeric"
})

html`<div>${git_history_table}</div>`

html`<div>${git_history_plot}</div>`

SHA	Date	Author	Description
005d89b	2023-12-20 17:23:04	Lino Galiana	Finalise l’affichage des statistiques Git (#478)
3fba612	2023-12-17 18:16:42	Lino Galiana	Remove some badges from python (#476)
7d12af8	2023-12-05 10:30:08	linogaliana	Modularise la partie import pour l’avoir partout
417fb66	2023-12-04 18:49:21	Lino Galiana	Corrections partie ML (#468)
1684220	2023-12-02 12:06:40	Antoine Palazzolo	Première partie de relecture de fin du cours (#467)
1f23de2	2023-12-01 17:25:36	Lino Galiana	Stockage des images sur S3 (#466)
a06a268	2023-11-23 18:23:28	Antoine Palazzolo	2ème relectures chapitres ML (#457)
b68369d	2023-11-18 18:21:13	Lino Galiana	Reprise du chapitre sur la classification (#455)
889a71b	2023-11-10 11:40:51	Antoine Palazzolo	Modification TP 3 (#443)
a771183	2023-10-09 11:27:45	Antoine Palazzolo	Relecture TD2 par Antoine (#418)
9a4e226	2023-08-28 17:11:52	Lino Galiana	Action to check URL still exist (#399)
3bdf3b0	2023-08-25 11:23:02	Lino Galiana	Simplification de la structure 🤓 (#393)
78ea2cb	2023-07-20 20:27:31	Lino Galiana	Change titles levels (#381)
29ff3f5	2023-07-07 14:17:53	linogaliana	description everywhere
f21a24d	2023-07-02 10:58:15	Lino Galiana	Pipeline Quarto & Pages 🚀 (#365)
8d81b5f	2023-02-18 18:21:59	Lino Galiana	Change source get_vectorfile (#355)
2ed4aa7	2022-11-07 15:57:31	Lino Galiana	Reprise 2e partie ML + Règle problème mathjax (#319)
a26b865	2022-09-03 15:34:28	linogaliana	Fix problem with SVM wikipedia image
f10815b	2022-08-25 16:00:03	Lino Galiana	Notebooks should now look more beautiful (#260)
494a85a	2022-08-05 14:49:56	Lino Galiana	Images featured ✨ (#252)
d201e3c	2022-08-03 15:50:34	Lino Galiana	Pimp la homepage ✨ (#249)
12965ba	2022-05-25 15:53:27	Lino Galiana	:launch: Bascule vers quarto (#226)
9c71d6e	2022-03-08 10:34:26	Lino Galiana	Plus d’éléments sur S3 (#218)
09b60a1	2021-12-21 19:58:58	Lino Galiana	Relecture suite du NLP (#205)
c3bf4d4	2021-12-06 19:43:26	Lino Galiana	Finalise debug partie ML (#190)
fb14d40	2021-12-06 17:00:52	Lino Galiana	Modifie l’import du script (#187)
37ecfa3	2021-12-06 14:48:05	Lino Galiana	Essaye nom différent (#186)
2c8fd0d	2021-12-06 13:06:36	Lino Galiana	Problème d’exécution du script import data ML (#185)
5d0a5e3	2021-12-04 07:41:43	Lino Galiana	MAJ URL script recup data (#184)
5c10490	2021-12-03 17:44:08	Lino Galiana	Relec @antuki partie modelisation (#183)
2a8809f	2021-10-27 12:05:34	Lino Galiana	Simplification des hooks pour gagner en flexibilité et clarté (#166)
2e4d586	2021-09-02 12:03:39	Lino Galiana	Simplify badges generation (#130)
0a14dfa	2021-07-07 15:17:11	Lino Galiana	Régler bug sc_recall (#119)
4cdb759	2021-05-12 10:37:23	Lino Galiana	:sparkles: :star2: Nouveau thème hugo :snake: :fire: (#105)
7f9f97b	2021-04-30 21:44:04	Lino Galiana	🐳 + 🐍 New workflow (docker 🐳) and new dataset for modelization (2020 🇺🇸 elections) (#99)
671f75a	2020-10-21 15:15:24	Lino Galiana	Introduction au Machine Learning (#72)

git_history_table = Inputs.table(
  table_commit,
  {
    format: {
      SHA: x => md`[${x}](${github_repo}/commit/${x})`,
      Description: x => md`${replacePullRequestPattern(x, github_repo)}`,
      /*Date: x => x.toLocaleString("fr", {
        "month": "numeric",
        "day": "numeric",
        "year": "numeric"
        })
      */
    }
  }
)

git_history_plot = Plot.plot({
  marks: [
    Plot.ruleY([0], {stroke: "royalblue"}),
    Plot.dot(
          table_commit,
          Plot.pointerX({x: (d) => new Date(d.date), y: 0, stroke: "red"})),
    Plot.dot(table_commit, {x: (d) => new Date(d.Date), y: 0, fill: "royalblue"})
  ]
})

function replacePullRequestPattern(inputString, githubRepo) {
    // Use a regular expression to match the pattern #digit
    var pattern = /#(\d+)/g;

    // Replace the pattern with ${github_repo}/pull/#digit
    var replacedString = inputString.replace(pattern, '[#$1](' + githubRepo + '/pull/$1)');

    return replacedString;
}

github_repo = "https://github.com/linogaliana/python-datascientist"

table_commit = {

// Get the HTML table by its class name
var table = document.querySelector('.commit-table');

// Check if the table exists
if (table) {
    // Initialize an array to store the table data
    var dataArray = [];

    // Extract headers from the first row
    var headers = [];
    for (var i = 0; i < table.rows[0].cells.length; i++) {
        headers.push(table.rows[0].cells[i].textContent.trim());
    }

    // Iterate through the rows, starting from the second row
    for (var i = 1; i < table.rows.length; i++) {
        var row = table.rows[i];
        var rowData = {};

        // Iterate through the cells in the row
        for (var j = 0; j < row.cells.length; j++) {
            // Use headers as keys and cell content as values
            rowData[headers[j]] = row.cells[j].textContent.trim();
        }

        // Push the rowData object to the dataArray
        dataArray.push(rowData);
    }
  }

  return dataArray

}

// Get the element with class 'git-details'
{
  var gitDetails = document.querySelector('.commit-table');

  // Check if the element exists
  if (gitDetails) {
      // Hide the element
      gitDetails.style.display = 'none';
  }
}

Plot = require('@observablehq/plot@0.6.12/dist/plot.umd.min.js')

Retour au sommet

Citation

BibTeX

@book{galiana2023,
  author = {Galiana, Lino},
  title = {Python pour la data science},
  date = {2023},
  url = {https://pythonds.linogaliana.fr/},
  doi = {10.5281/zenodo.8229676},
  langid = {fr}
}

Veuillez citer ce travail comme suit :

Galiana, Lino. 2023. Python pour la data science. https://doi.org/10.5281/zenodo.8229676.