Numpy, la brique de base de la data science

Numpy constitue la brique de base de l’écosystème de la data science en Python. Toutes les librairies de manipulation de données, de modélisation et de visualisation reposent, de manière plus ou moins directe, sur Numpy. Il est donc indispensable de revoir quelques notions sur ce package avant d’aller plus loin.

Auteur·rice

Lino Galiana

Date de publication

2026-01-11

Pour essayer les exemples présents dans ce tutoriel :
View on GitHub Onyxia Onyxia Open In Colab

1 Introduction

Ce chapitre constitue une introduction à Numpy pour s’assurer que les bases du calcul vectoriel avec Python soient maîtrisées. La première partie du chapitre présente des petits exercices pour pratiquer quelques fonctions basiques de Numpy. La fin du chapitre présente des exercices pratiques d’utilisation de Numpy plus approfondis.

Il est recommandé de régulièrement se référer à la cheatsheet numpy et à la doc officielle en cas de doute sur une fonction.

Dans ce chapitre, on ne dérogera pas à la convention qui s’est imposée d’importer Numpy de la manière suivante :

import numpy as np

Nous allons également fixer la racine du générateur aléatoire de nombres afin d’avoir des résultats reproductibles :

import numpy as np
rng = np.random.default_rng(seed=12345)
Mise en gardeCaution

Historiquement, la génération de nombres aléatoires se faisait pas le biais du package numpy.random. Néanmoins, les auteurs de Numpy recommandent maintenant d’utiliser plutôt des générateurs pour cela. Les exemples de ce tutoriel adoptent donc cette pratique.

2 Le concept d’array

Dans le monde de la science des données, comme cela sera évoqué plus en profondeur dans les prochains chapitres, l’objet central est le tableau à deux dimensions de données. La première correspond aux lignes et la seconde aux colonnes. Si on ne se préoccupe que d’une dimension, on se rapporte à une variable (une colonne) de notre tableau de données. Il est donc naturel de faire le lien entre les tableaux de données et l’objet mathématique que sont les matrices et les vecteurs.

NumPy (Numerical Python) est la brique de base pour traiter des listes numériques ou des chaines de textes comme des matrices. NumPy intervient pour proposer ce type d’objets, et les opérations standardisées associées qui n’existent pas dans le langage Python de base.

L’objet central de NumPy est l’array qui est un tableau de données multidimensionnel. L’array Numpy peut être unidimensionnel et s’apparenter à un vecteur (1d-array), bidimensionnel et ainsi s’apparenter à une matrice (2d-array) ou, de manière plus générale, prendre la forme d’un objet multidimensionnel (Nd-array), sorte de tableau emboîté.

Les tableaux simples (uni ou bi-dimensionnels) sont faciles à se représenter et représentent la majorité des besoins liés à Numpy. Nous découvrirons lors du chapitre suivant, sur Pandas, qu’en pratique on manipule rarement directement Numpy qui est une librairie bas niveau. Un DataFrame Pandas sera construit à partir d’une collection d’array uni-dimensionnels (les variables de la table), ce qui permettra d’effectuer des opérations cohérentes (et optimisées) avec le type de la variable. Avoir quelques notions Numpy est utile pour comprendre la logique de manipulation vectorielle rendant les traitements sur des données plus lisibles, plus efficaces et plus fiables.

Par rapport à une liste,

  • un array ne peut contenir qu’un type de données (integer, string, etc.), contrairement à une liste.
  • les opérations implémentées par Numpy seront plus efficaces et demanderont moins de mémoire

Les données géographiques constitueront une construction un peu plus complexe qu’un DataFrame traditionnel. La dimension géographique prend la forme d’un tableau plus profond, au moins bidimensionnel (coordonnées d’un point). Néanmoins, les librairies de manipulation de données géographiques permettront de ne pas se préoccuper de cette complexité accrue.

2.1 Créer un array

On peut créer un array de plusieurs manières. Pour créer un array à partir d’une liste, il suffit d’utiliser la méthode array:

np.array([1,2,5])
array([1, 2, 5])

Il est possible d’ajouter un argument dtype pour contraindre le type du array :

np.array([["a","z","e"],["r","t"],["y"]], dtype="object")
array([list(['a', 'z', 'e']), list(['r', 't']), list(['y'])], dtype=object)

Il existe aussi des méthodes pratiques pour créer des array:

  • séquences logiques : np.arange (suite) ou np.linspace (interpolation linéaire entre deux bornes) ;
  • séquences ordonnées : array rempli de zéros, de 1 ou d’un nombre désiré : np.zeros, np.ones ou np.full ;
  • séquences aléatoires : fonctions de génération de nombres aléatoires : rng.uniform, rng.normal, etc. où rng est un générateur de nombre aléatoires ;
  • tableau sous forme de matrice identité : np.eye.

Ceci donne ainsi, pour les séquences logiques:

np.arange(0,10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.arange(0,10,3)
array([0, 3, 6, 9])
np.linspace(0, 1, 5)
array([0.  , 0.25, 0.5 , 0.75, 1.  ])

Pour un array initialisé à 0:

np.zeros(10, dtype=int)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

ou initialisé à 1:

np.ones((3, 5), dtype=float)
array([[1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1.]])

ou encore initialisé à 3.14:

np.full((3, 5), 3.14)
array([[3.14, 3.14, 3.14, 3.14, 3.14],
       [3.14, 3.14, 3.14, 3.14, 3.14],
       [3.14, 3.14, 3.14, 3.14, 3.14]])

Enfin, pour créer la matrice \(I_3\):

np.eye(3)
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
AstuceExercice 1

Générer:

  • \(X\) une variable aléatoire, 1000 répétitions d’une loi \(U(0,1)\)
  • \(Y\) une variable aléatoire, 1000 répétitions d’une loi normale de moyenne nulle et de variance égale à 2
  • Vérifier la variance de \(Y\) avec np.var

3 Indexation et slicing

3.1 Logique dans le cas d’un array unidimensionnel

La structure la plus simple est l’array unidimensionnel:

x = np.arange(10)
print(x)
[0 1 2 3 4 5 6 7 8 9]

L’indexation est dans ce cas similaire à celle d’une liste:

  • le premier élément est 0
  • le énième élément est accessible à la position \(n-1\)

La logique d’accès aux éléments est ainsi la suivante :

x[start:stop:step]

Avec un array unidimensionnel, l’opération de slicing (garder une coupe du array) est très simple. Par exemple, pour garder les K premiers éléments d’un array, on fera:

x[:K]

En l’occurrence, on sélectionne le K\(^{eme}\) élément en utilisant

x[K-1]

Pour sélectionner uniquement un élément, on fera ainsi:

x = np.arange(10)
x[2]
np.int64(2)

Les syntaxes qui permettent de sélectionner des indices particuliers d’une liste fonctionnent également avec les arrays.

AstuceExercice 2

Prenez x = np.arange(10) et…

  • Sélectionner les éléments 0, 3, 5 de x
  • Sélectionner les éléments pairs
  • Sélectionner tous les éléments sauf le premier
  • Sélectionner les 5 premiers éléments
np.arange(10)
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

La logique se généralise pour les array multidimensionnels. L’indexation se fait alors à plusieurs niveaux. Prenons par exemple un array à 2 dimensions (une matrice en quelques sortes):

x = np.array([[1, 2, 3], [4, 5, 6]], np.int32)

Si on veut sélectionner la 2e ligne, 3e colonne (l’élément de valeur 6), on fait

x[1, 2]
np.int32(6)

Maintenant, pour sélectionner une colonne complète (par exemple la 2e), on peut utiliser le 2e index pour spécifier celle-ci (index 1 en Python puisque l’indexation part de 0) puis : sur la première dimension (version raccourcie de 0:N) pour ne pas discriminer selon cette dimension:

x[:,1]
array([2, 5], dtype=int32)

Le principe se généralise, mais se complexifie, pour des array imbriqués. Heureusement, ce sont des objets qu’on manipule assez rarement directement, la plupart de nos données numériques étant des tableaux plats (une valeur - l’observation - est le croisement d’une ligne - l’individu - et d’une colonne - la variable).

3.2 Sur la performance

Un élément déterminant dans la performance de Numpy par rapport aux listes, lorsqu’il est question de slicing est qu’un array ne renvoie pas une copie de l’élément en question (copie qui coûte de la mémoire et du temps) mais simplement une vue de celui-ci.

Lorsqu’il est nécessaire d’effectuer une copie, par exemple pour ne pas altérer l’array sous-jacent, on peut utiliser la méthode copy:

x_sub_copy = x[:2, :2].copy()

3.3 Filtres logiques

Il est également possible, et plus pratique, de sélectionner des données à partir de conditions logiques (opération qu’on appelle un boolean mask). Cette fonctionalité servira principalement à effectuer des opérations de filtre sur les données.

Pour des opérations de comparaison simples, les comparateurs logiques peuvent être suffisants. Ces comparaisons fonctionnent aussi sur les tableaux multidimensionnels grâce au broadcasting sur lequel nous reviendrons :

x = np.arange(10)
x2 = np.array([[-1,1,-2],[-3,2,0]])
print(x)
print(x2)
[0 1 2 3 4 5 6 7 8 9]
[[-1  1 -2]
 [-3  2  0]]
x==2
x2<0
array([[ True, False,  True],
       [ True, False, False]])

Pour sélectionner les observations relatives à la condition logique, il suffit d’utiliser la logique de slicing de numpy qui fonctionne avec les conditions logiques

AstuceExercice 3

Soit

x = np.random.normal(size=10000)
  1. Ne conserver que les valeurs dont la valeur absolue est supérieure à 1.96
  2. Compter le nombre de valeurs supérieures à 1.96 en valeur absolue et leur proportion dans l’ensemble
  3. Sommer les valeurs absolues de toutes les observations supérieures (en valeur absolue) à 1.96 et rapportez les à la somme des valeurs de x (en valeur absolue)

Lorsque c’est possible, il est recommandé d’utiliser les fonctions logiques de numpy (optimisées et qui gèrent bien la dimension). Parmi elles, on peut retrouver:

  • count_nonzero ;
  • isnan ;
  • any ou all, notamment avec l’argument axis ;
  • np.array_equal pour vérifier, élément par élément, l’égalité.

Soient x un array multidimensionnel et y un array unidimensionnel présentant une valeur manquante.

# Assuming rng has been created beforehand
x = rng.normal(0, size=(3, 4))
y = np.array([np.nan, 0, 1])
AstuceExercice 4
  1. Utiliser count_nonzero sur y
  2. Utiliser isnan sur y et compter le nombre de valeurs non NaN
  3. Vérifier que x comporte au moins une valeur positive dans son ensemble, en parcourant les lignes puis les colonnes.
Aide

Jetez un oeil au paramètre axis en vous documentant sur internet. Par exemple ici.

4 Manipuler un array

4.1 Fonctions de manipulation

Numpy propose des méthodes ou des fonctions standardisées pour modifier un array, voici un tableau en présentant quelques-unes:

Opération Implémentation
Aplatir un array x.flatten() (méthode)
Transposer un array x.T (méthode) ou np.transpose(x) (fonction)
Ajouter des éléments à la fin np.append(x, [1,2])
Ajouter des éléments à un endroit donné (aux positions 1 et 2) np.insert(x, [1,2], 3)
Supprimer des éléments (aux positions 0 et 3) np.delete(x, [0,3])

Pour combiner des array, on peut utiliser, selon les cas, les fonctions np.concatenate, np.vstack ou la méthode .r_ (concaténation rowwise). np.hstack ou la méthode .column_stack ou .c_ (concaténation column-wise)

x = rng.normal(size = 10)

Pour ordonner un array, on utilise np.sort

x = np.array([7, 2, 3, 1, 6, 5, 4])

np.sort(x)
array([1, 2, 3, 4, 5, 6, 7])

Si on désire faire un ré-ordonnement partiel pour trouver les k valeurs les plus petites d’un array sans les ordonner, on utilise partition:

np.partition(x, 3)
array([1, 2, 3, 4, 5, 6, 7])

4.2 Statistiques sur un array

Pour les statistiques descriptives classiques, Numpy propose un certain nombre de fonctions déjà implémentées, qui peuvent être combinées avec l’argument axis

x = rng.normal(0, size=(3, 4))
AstuceExercice 5
  1. Faire la somme de tous les éléments d’un array, des éléments en ligne et des éléments en colonne. Vérifier la cohérence.
  2. Ecrire une fonction statdesc pour renvoyer les valeurs suivantes : moyenne, médiane, écart-type, minimum et maximum. L’appliquer sur x en jouant avec l’argument axis

5 Simulations numériques

Numpy est incontournable dès lors qu’on effectue des simulations aléatoires, ce qui est très commun en statistiques computationnelles avec un ensemble de méthodes dites de Monte-Carlo. Le principe général est de remplacer un calcul théorique difficile (une intégrale, une probabilité, une espérance) par une approximation numérique obtenue en répétant un grand nombre de tirages aléatoires et en moyennant la quantité d’intérêt, en s’appuyant sur la loi des grands nombres et le théorème central limite pour quantifier la précision de l’estimation.

Illustrons empiriquement quelques théorèmes incontournables de la statistique par une série d’exercices. Cela permettra d’explorer :

  • La loi des grands nombres (?@tip-exo2fr);
  • Le théorème central limite et sa version particulière dans le cas de lancer de pièce, le théorème de Moivre-Laplace ;
  • Les intervalles de confiance théoriques et leur contrepartie empirique à travers le bootstrap ;
  • Le principe des méthodes de Monte Carlo avec l’algorithme du rejet.

Nous allons avoir besoin des éléments suivants pour initialiser notre processus générateur de données.

import numpy as np

def generate_grid(size_max=1000):
    n_small = np.arange(3, 200, 2)
    n_log = np.unique(np.round(np.logspace(np.log10(200), np.log10(size_max), 120)).astype(int))
    return np.unique(np.concatenate([n_small, n_log]))

N_max = 100_000
rng = np.random.default_rng(seed=123)
grid = generate_grid(size_max=N_max)

Ces éléments nous permettent de générer une série aléatoire d’observations jusqu’à une taille N_max, puis d’observer l’évolution des estimateurs empiriques de moments (moyenne et variance) lorsque l’on ne conserve que les n premières observations, pour différents n donnés par grid. L’objectif est d’illustrer la convergence des estimateurs empiriques vers leurs valeurs théoriques lorsque n augmente.

5.1 Loi des grands nombres

Nous sommes accoutumés à faire le lien, assez intuitif, entre la théorie des probabilités et la statistique. C’est notamment possible grâce à des théorèmes comme le théorème fondamental de la statistique (théorème de Glivenko-Cantelli). Cette relation est le fondement de la science des données, et plus globalement de la statistique, dans sa dimension inférentielle comme descriptive, puisque sans des intuitions mathématiques formelles nous aurions du mal à généraliser les interprétations issues de données observées.

La loi des grands nombres peut être illustrée assez facilement par le biais de simulations numériques. Nous allons simuler une suite répétée de tirages aléatoires, ce sera l’équivalent pratique de la suite i.i.d \((X)_i\) du théorème.

AstuceExercice 6: la loi des grands nombres

On considère une suite i.i.d. \((X_i)_{i \ge 1}\) telle que \(X_i \sim \mathcal{U}\bigl([0,1]\bigr)\).

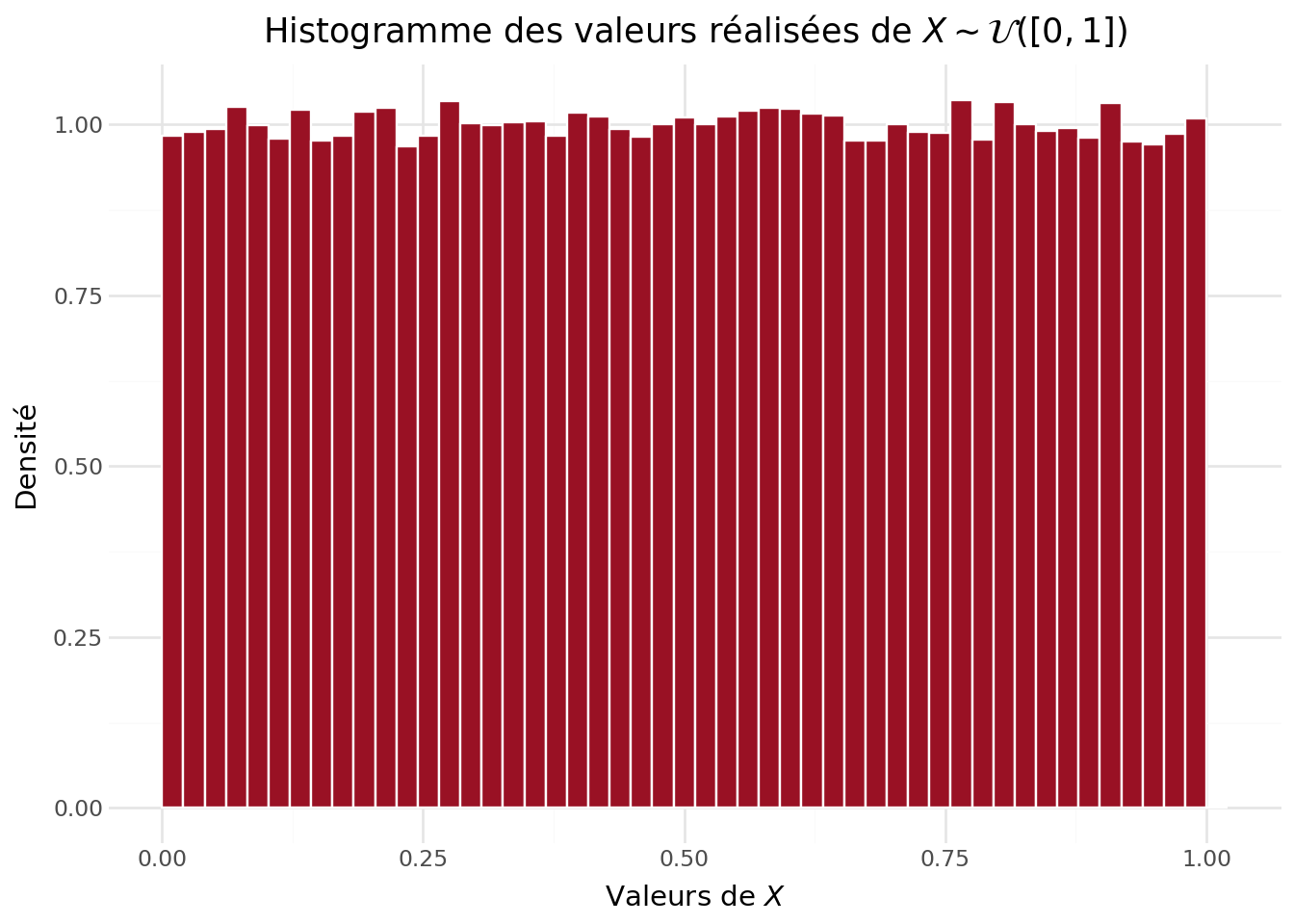
  1. Générer un vecteur X de taille N_max suivant la loi uniforme \(\mathcal{U}\bigl([0,1]\bigr)\).
  2. Représenter l’histogramme des valeurs observées \(X_i\).
  3. Pour chaque valeur \(n\) de grid, calculer les grandeurs empiriques associées au préfixe \((X_1,\dots,X_n)\):
Notation Nom Formule Remarque
\(\bar X_n\) ou \(\widehat{\mu}\) Moyenne empirique \(\displaystyle \bar X_n=\frac{1}{n}\sum_{i=1}^{n}X_i\) Estime l’espérance \(\mathbb{E}[X]=\mu\).
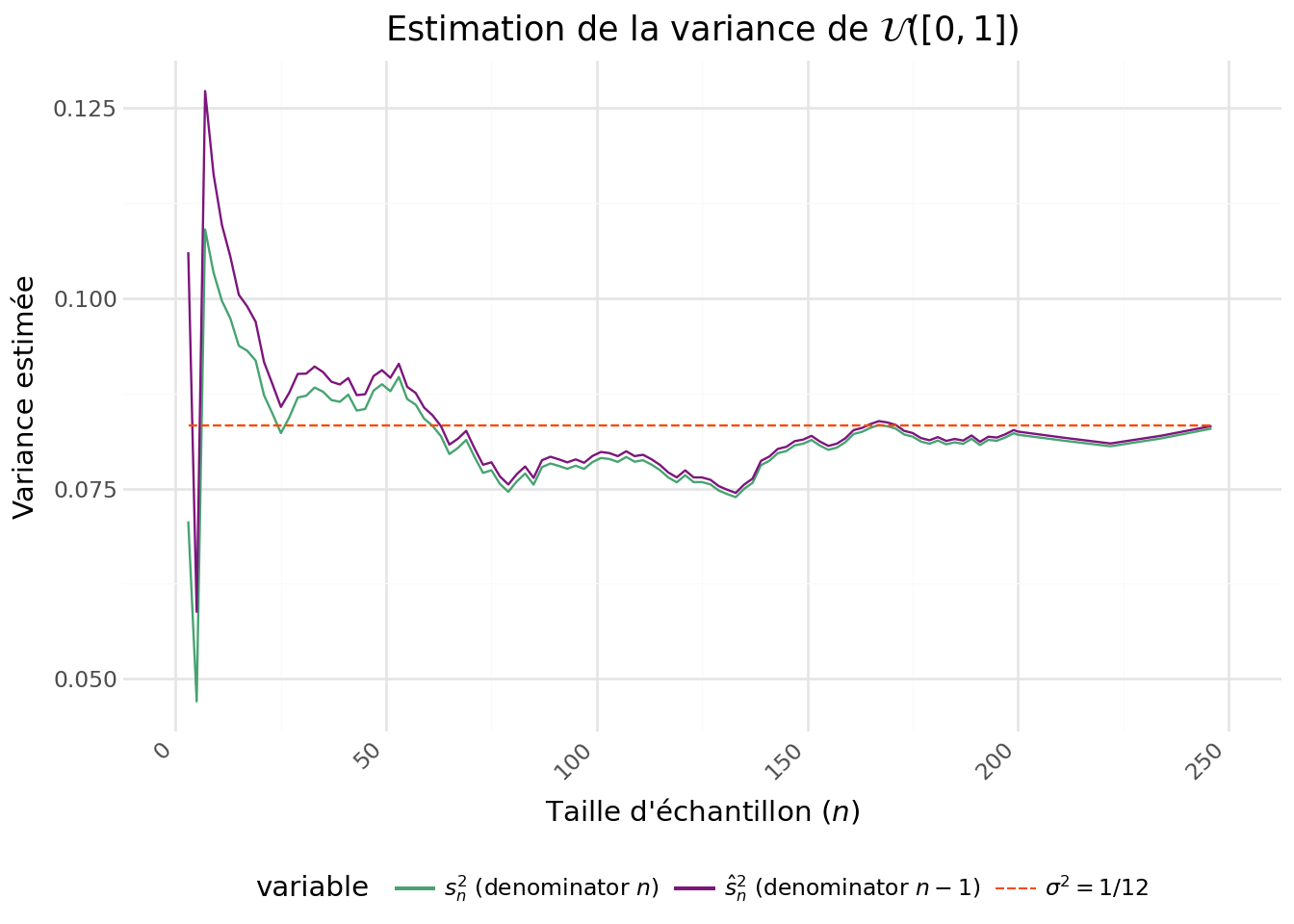
\(s_n^2\) Variance empirique (diviseur \(n\)) \(\displaystyle s_n^2=\frac{1}{n}\sum_{i=1}^{n}(X_i-\bar X_n)^2\) Version “naïve” (souvent biaisée pour \(\mathrm{Var}(X)=\sigma^2\)).
\(\hat s_n^2\) Variance d’échantillon non biaisée (diviseur \(n-1\)) \(\displaystyle \hat s_n^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar X_n)^2\) Estimateur non biaisé de \(\mathrm{Var}(X)=\sigma^2\) (sous i.i.d.).
  1. Rappeler les valeurs théoriques de la moyenne \(\mu\) et de la variance \(\sigma^2\) de \(\mathcal{U}\bigl([0,1]\bigr)\), puis comparer graphiquement les quantités empiriques à ces valeurs.
  2. À quelle vitesse la moyenne empirique \(\bar X_n\) converge-t-elle vers \(\mu\) ? Proposer une illustration graphique (par exemple en traçant \(|\bar X_n-\mu|\) en fonction de \(n\) et en comparant à une décroissance en \(1/\sqrt{n}\), ou en traçant \(\sqrt{n}\,|\bar X_n-\mu|\)).

La densité empirique sur notre tirage de grande taille montre bien une quasi-équirépartition des valeurs (Figure 5.1). Notre loi empirique n’est pas parfaitement uniforme mais n’est pas loin de l’être à vue d’oeil. Avant d’étudier plus amplement la distribution, objet des prochains exercices, on peut déjà vérifier les moments de notre tirage que sont la moyenne et la variance empirique.

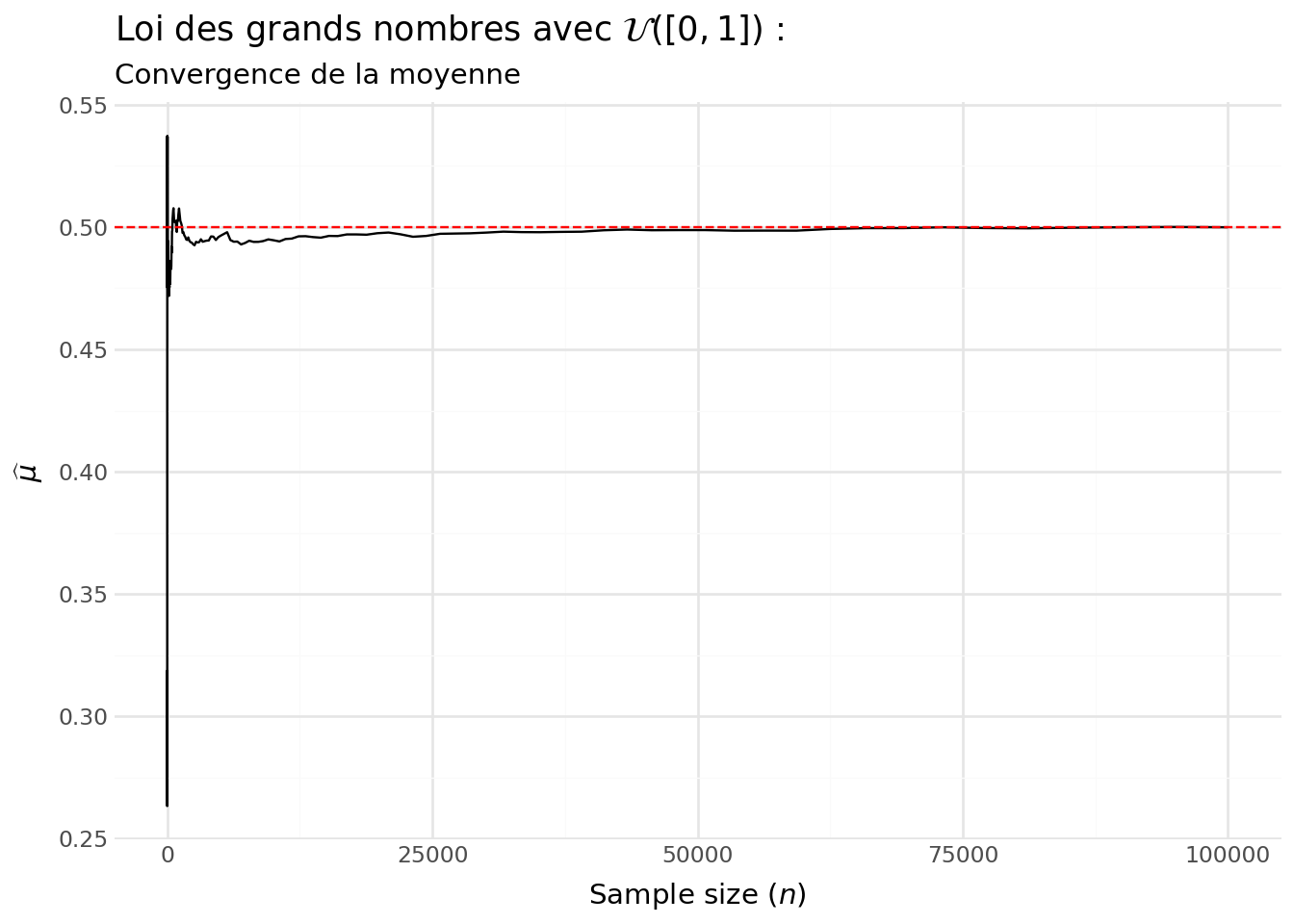
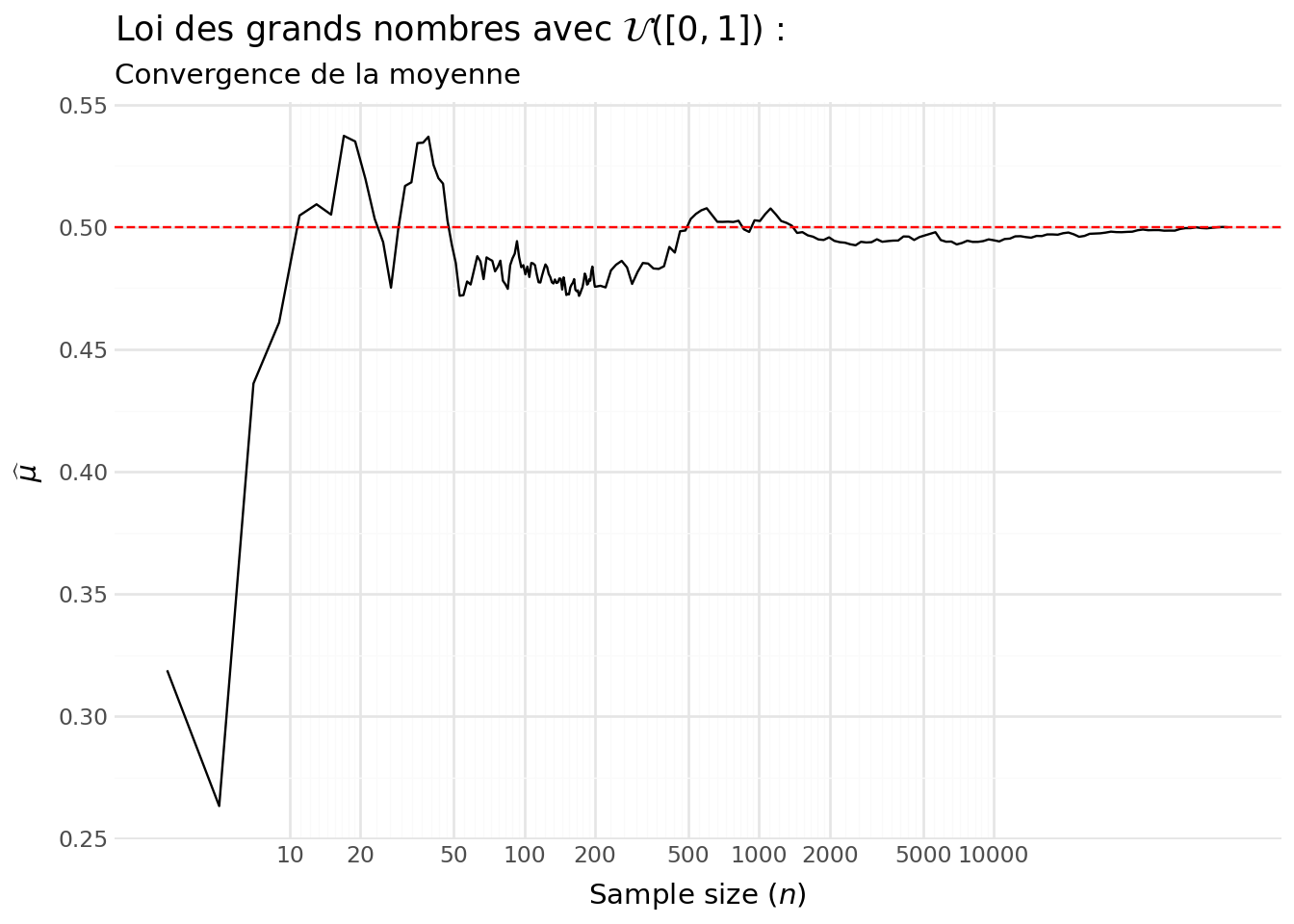
Figure 5.1: Distribution empirique de notre tirage aléatoire de loi uniforme (question 2, ?@tip-exo2-fr)

Avec la Figure 5.2, on voit la convergence de la moyenne empirique vers sa valeur théorique (l’espérance).

<>:5: SyntaxWarning: invalid escape sequence '\w'
<>:5: SyntaxWarning: invalid escape sequence '\w'
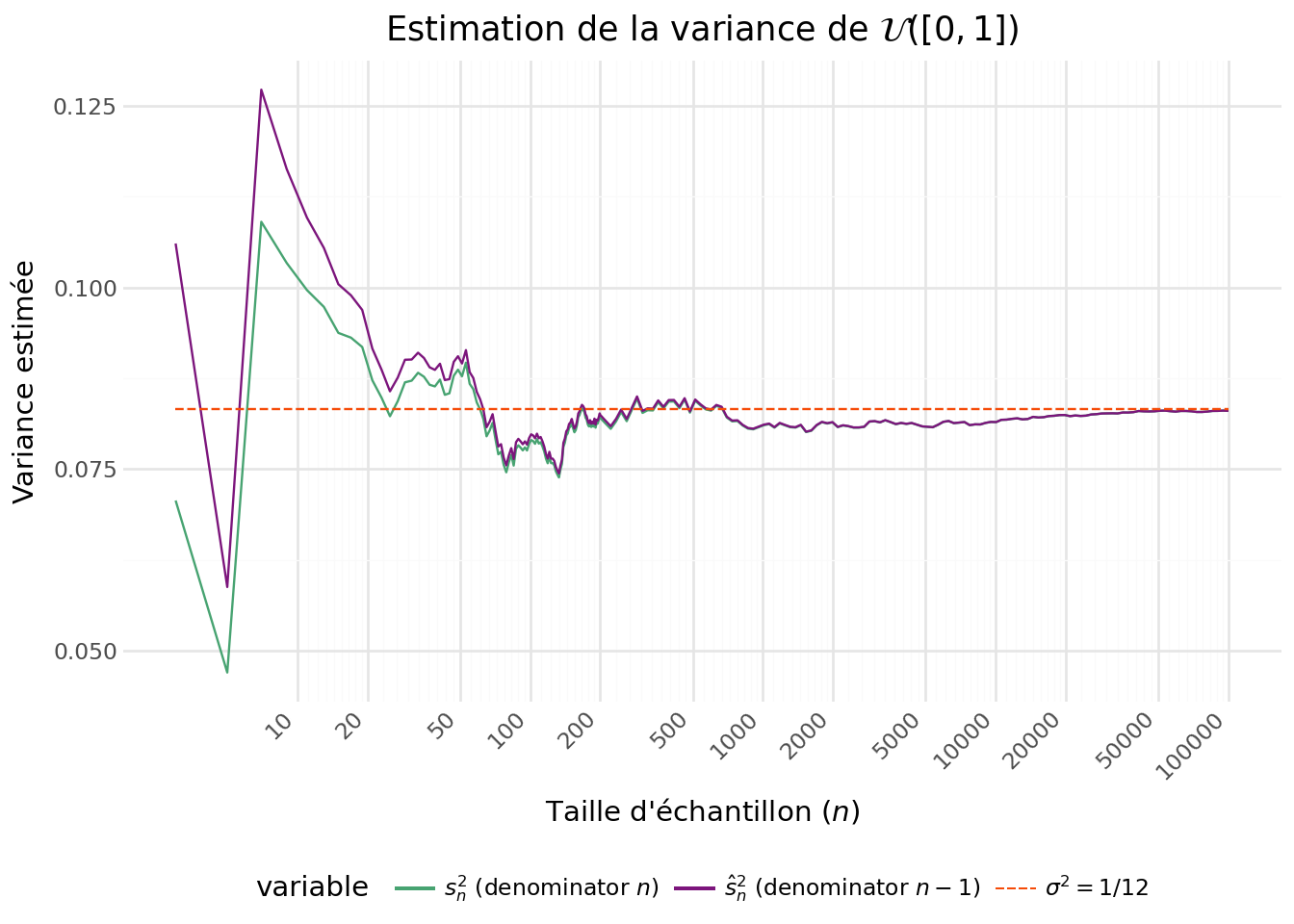
/tmp/ipykernel_6257/3615663993.py:5: SyntaxWarning: invalid escape sequence '\w'
(a) Echelle normale
(b) Echelle logarithmique
Figure 5.2: Convergence de la moyenne vers l’espérance théorique (question 3, ?@tip-exo2-fr)

Avec la Figure 5.3 on voit que la version intuitive de la variance empirique, c’est-à-dire celle avec \(n\) au dénominateur, tend à systématiquement sous-estimer la variance. Il s’agit en effet d’un estimateur biaisé, même si celui-ci tend vers 0 à mesurer que \(n\) croît. La variance d’échantillon, celle avec \(n-1\), suit globalement la même dynamique mais se rapproche plus tôt de la valeur théorique.

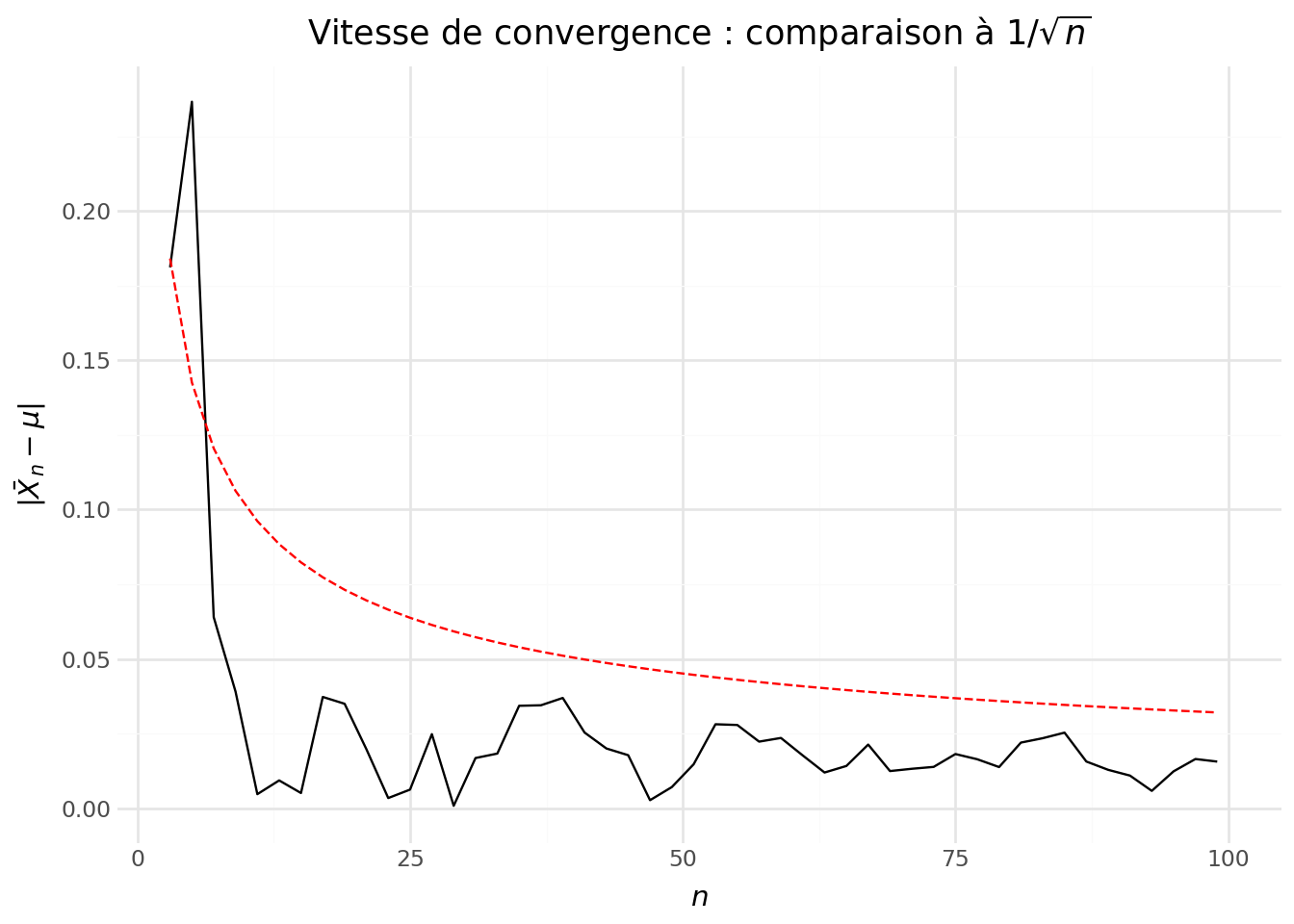
/home/runner/work/python-datascientist/python-datascientist/.venv/lib/python3.13/site-packages/plotnine/geoms/geom_path.py:100: PlotnineWarning: geom_path: Removed 115 rows containing missing values.
(a) Echelle normale
(b) Zoom sur les premières observations
Figure 5.3: Convergence de la variance empirique vers la variance théorique (question 3, ?@tip-exo2-fr)

Regardons la différence, en valeur absolue, entre \(\mu\) et \(\widehat{\mu}\) pour essayer de déterminer la vitesse de convergence. Faisons ceci pour les premières valeurs, celles avant que l’erreur d’estimation soit minime.

/home/runner/work/python-datascientist/python-datascientist/.venv/lib/python3.13/site-packages/plotnine/geoms/geom_path.py:100: PlotnineWarning: geom_path: Removed 170 rows containing missing values.
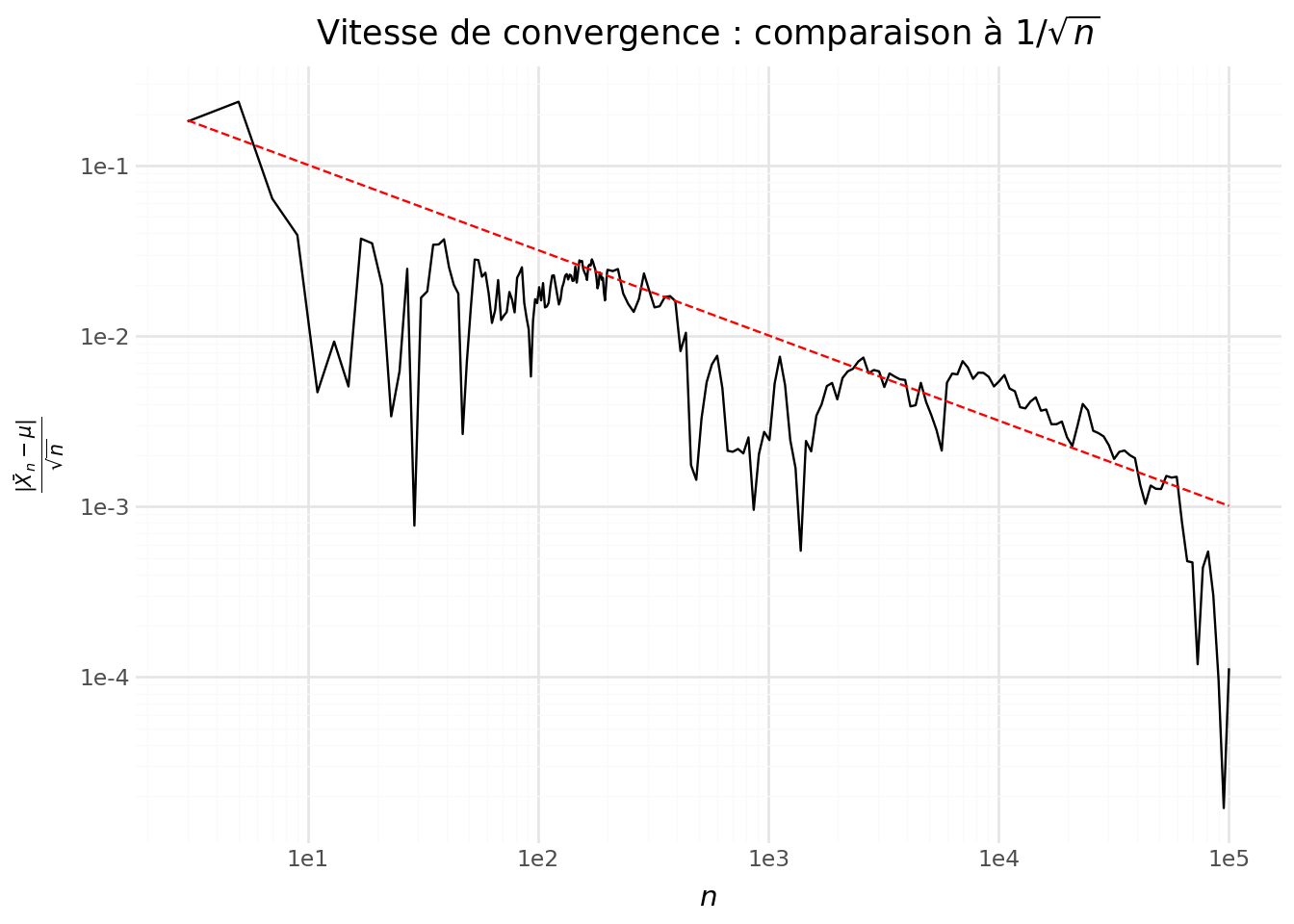
/home/runner/work/python-datascientist/python-datascientist/.venv/lib/python3.13/site-packages/plotnine/geoms/geom_path.py:100: PlotnineWarning: geom_path: Removed 170 rows containing missing values.

Cela ressemble à une hyperbole du type \(1/\sqrt{n}\). Vérifions si cela est cohérent en représentant \(|\bar X_n - \mu|/\sqrt{n}\). Si on représente, au-delà des premières valeurs, le rapport entre l’erreur d’estimation et \(\sqrt{n}\) (Figure 5.4), on voit que l’intuition précédente était correcte. On a bien une erreur d’estimation qui oscille autour de \(\sqrt{n}\).

Figure 5.4: Représentation de l’erreur d’estimation et son lien avec le nombre d’observations

5.2 Distribution de résultats de lancer de pièces

AstuceExercice 6, partie 2. Moivre-Laplace (binomiale)

On considère une suite i.i.d. \((X_i)_{i \ge 1}\) telle que \(X_i \sim \mathcal{B}(100,1/2)\) (nombre de piles sur 100 lancers d’une pièce équilibrée).

  1. Représenter graphiquement la loi de \(X_1\) (fonction de masse) : \(k \mapsto \mathbb{P}(X_1=k)\) pour \(k \in \{0,\dots,100\}\).
  2. Calculer la moyenne \(\mu=\mathbb{E}[X_1]\) et la variance \(\sigma^2=\mathrm{Var}(X_1)\). Donner leurs valeurs numériques.
  3. Pour une valeur \(N\) (par exemple \(N \in \{50,200,1000,5000\}\)), générer \(X_1,\dots,X_N\) i.i.d. et calculer \(\bar X_N = \frac{1}{N}\sum_{i=1}^N X_i\).
  4. En répétant l’expérience un grand nombre de fois, représenter la distribution empirique de \[ Y_N = \sqrt{N}\,(\bar X_N-\mu). \]
  5. Sur la même figure, superposer la densité de la loi normale \(\mathcal{N}(0,\sigma^2)\). Dans ce cas, on doit obtenir \(\sigma^2=25\).
AstuceExercice 6, partie 3. TCL pour d’autres lois (variance finie)

Choisir une loi parmi : Poisson, exponentielle, uniforme (au choix), en précisant ses paramètres. On considère une suite i.i.d. \((X_i)_{i \ge 1}\) suivant cette loi, de moyenne \(\mu\) et variance \(\sigma^2\) (finies).

  1. Donner (ou calculer) \(\mu\) et \(\sigma^2\) pour la loi choisie.
  2. Pour plusieurs valeurs de \(N\), en répétant l’expérience un grand nombre de fois, représenter la distribution empirique de \[ Y_N = \sqrt{N}\,(\bar X_N-\mu) \] et la comparer à la densité de la loi normale \(\mathcal{N}(0,\sigma^2)\).
  3. Option : étudier aussi la version standardisée \[ Z_N = \sqrt{N}\,\frac{\bar X_N-\mu}{\sigma} \] et la comparer à \(\mathcal{N}(0,1)\).
AstuceExercice 6, partie 4. Contre-exemple : loi de Cauchy

On considère maintenant une suite i.i.d. \((X_i)_{i \ge 1}\) suivant une loi de Cauchy standard.

  1. Générer un vecteur X de taille N_max suivant une loi de Cauchy standard.
  2. Pour chaque valeur \(n\) de grid, calculer la moyenne empirique \(\bar X_n = \frac{1}{n}\sum_{i=1}^n X_i\) et tracer \(\bar X_n\) en fonction de \(n\).
  3. Le comportement observé ressemble-t-il à une convergence vers une constante ? Comparer qualitativement avec la partie 1.
  4. La LGN et le TCL “classiques” s’appliquent-ils ici ? Justifier en discutant l’existence (ou non) de \(\mu\) et de \(\sigma^2\).

6 Broadcasting

Le broadcasting désigne un ensemble de règles permettant d’appliquer des opérations sur des tableaux de dimensions différentes. En pratique, cela consiste généralement à appliquer une seule opération à l’ensemble des membres d’un tableau numpy.

La différence peut être comprise à partir de l’exemple suivant. Le broadcasting permet de transformer le scalaire 5 en array de dimension 3:

a = np.array([0, 1, 2])
b = np.array([5, 5, 5])

a + b
a + 5
array([5, 6, 7])

Le broadcasting peut être très pratique pour effectuer de manière efficace des opérations sur des données à la structure complexe. Pour plus de détails, se rendre ici ou ici.

6.1 Une application: programmer ses propres k-nearest neighbors

AstuceExercice 6 (un peu plus corsé)
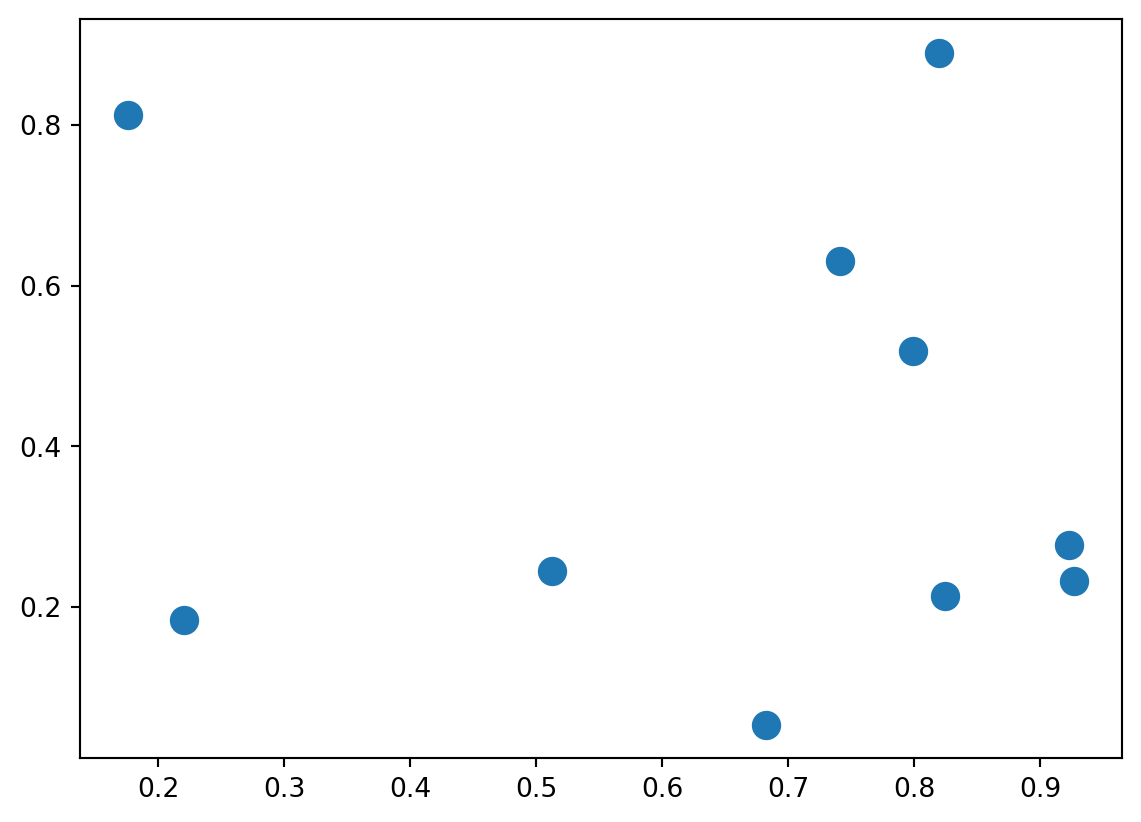
  1. Créer X un tableau à deux dimensions (i.e. une matrice) comportant 10 lignes et 2 colonnes. Les nombres dans le tableau sont aléatoires.
  2. Importer le module matplotlib.pyplot sous le nom plt. Utiliser plt.scatter pour représenter les données sous forme de nuage de points.
  3. Constuire une matrice 10x10 stockant, à l’élément \((i,j)\), la distance euclidienne entre les points \(X[i,]\) et \(X[j,]\). Pour cela, il va falloir jouer avec les dimensions en créant des tableaux emboîtés à partir par des appels à np.newaxis :
    1. En premier lieu, utiliser X1 = X[:, np.newaxis, :] pour transformer la matrice en tableau emboîté. Vérifier les dimensions
    2. Créer X2 de dimension (1, 10, 2) à partir de la même logique
    3. En déduire, pour chaque point, la distance avec les autres points pour chaque coordonnées. Elever celle-ci au carré
    4. A ce stade, vous devriez avoir un tableau de dimension (10, 10, 2). La réduction à une matrice s’obtient en sommant sur le dernier axe. Regarder dans l’aide de np.sum comme effectuer une somme sur le dernier axe.
    5. Enfin, appliquer la racine carrée pour obtenir une distance euclidienne en bonne et due forme.
  4. Vérifier que les termes diagonaux sont bien nuls (distance d’un point à lui-même…)
  5. Il s’agit maintenant de classer, pour chaque point, les points dont les valeurs sont les plus similaires. Utiliser np.argsort pour obtenir, pour chaque ligne, le classement des points les plus proches
  6. On va s’intéresser aux k-plus proches voisins. Pour le moment, fixons k=2. Utiliser argpartition pour réordonner chaque ligne de manière à avoir les 2 plus proches voisins de chaque point d’abord et le reste de la ligne ensuite
  7. Utiliser le morceau de code ci-dessous
Un indice pour représenter graphiquement les plus proches voisins 
plt.scatter(X[:, 0], X[:, 1], s=100)

# draw lines from each point to its two nearest neighbors
K = 2

for i in range(X.shape[0]):
    for j in nearest_partition[i, :K+1]:
        # plot a line from X[i] to X[j]
        # use some zip magic to make it happen:
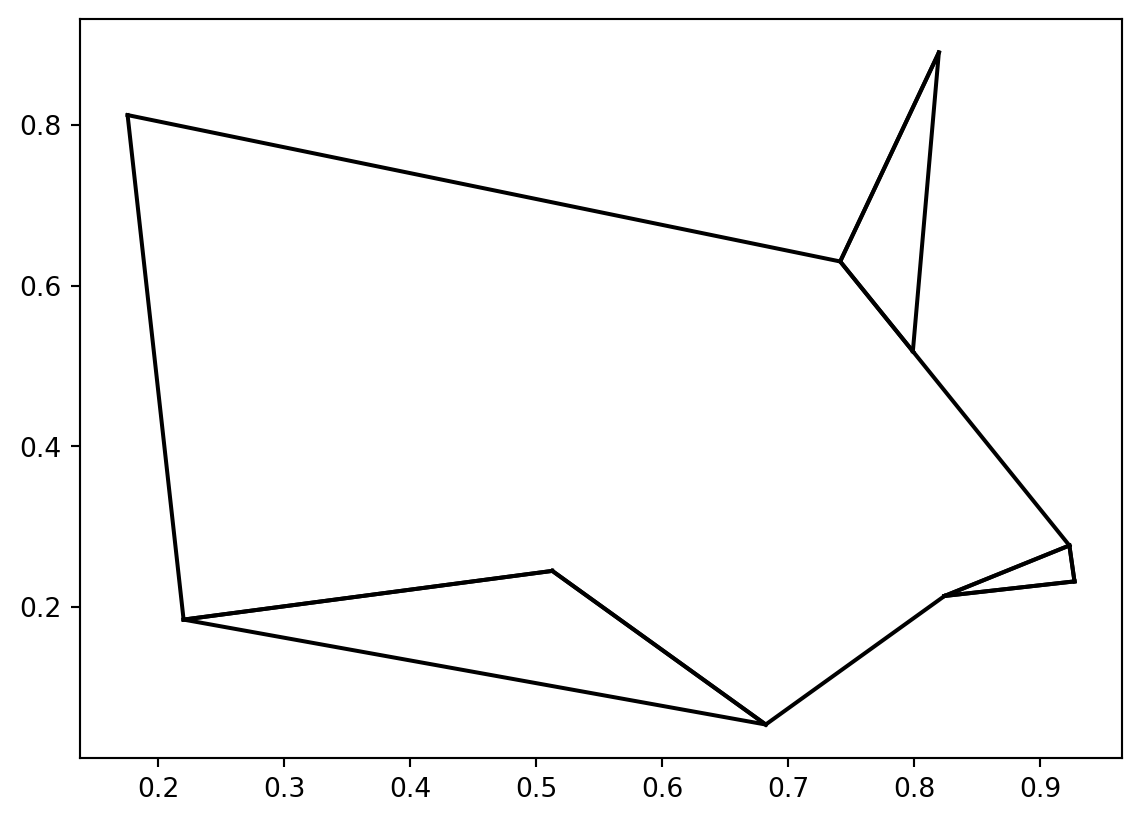
        plt.plot(*zip(X[j], X[i]), color='black')

Pour la question 2, vous devriez obtenir un graphique ayant cet aspect

For question 2, you should get a graph that looks like this:

Le résultat de la question 7 est le suivant :

Ai-je inventé cet exercice corsé ? Pas du tout, il vient de l’ouvrage Python Data Science Handbook. Mais, si je vous l’avais indiqué immédiatement, auriez-vous cherché à répondre aux questions ?

Par ailleurs, il ne serait pas une bonne idée de généraliser cet algorithme à de grosses données. La complexité de notre approche est \(O(N^2)\). L’algorithme implémenté par Scikit-Learn est en \(O[NlogN]\).

De plus, le calcul de distances matricielles en utilisant la puissance des cartes graphiques serait plus rapide. A cet égard, la librairie faiss ou les frameworks spécialisés dans le calcul de distance entre des vecteurs à haute dimension comme ChromaDB offrent des performances beaucoup plus satisfaisantes que celles que permettraient Numpy sur ce problème précis.

7 Exercices supplémentaires

AstuceComprendre le principe de l’algorithme PageRank

Google est devenu célèbre grâce à son algorithme PageRank. Celui-ci permet, à partir de liens entre sites web, de donner un score d’importance à un site web qui va être utilisé pour évaluer sa centralité dans un réseau. L’objectif de cet exercice est d’utiliser Numpy pour mettre en oeuvre un tel algorithme à partir d’une matrice d’adjacence qui relie les sites entre eux.

  1. Créer la matrice suivante avec Numpy. L’appeler M:

\[ \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0.5 & 0 & 0 & 0 & 0 \\ 0.5 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0.5 & 0 & 0 \\ 0 & 0 & 0.5 & 1 & 0 \end{bmatrix} \]

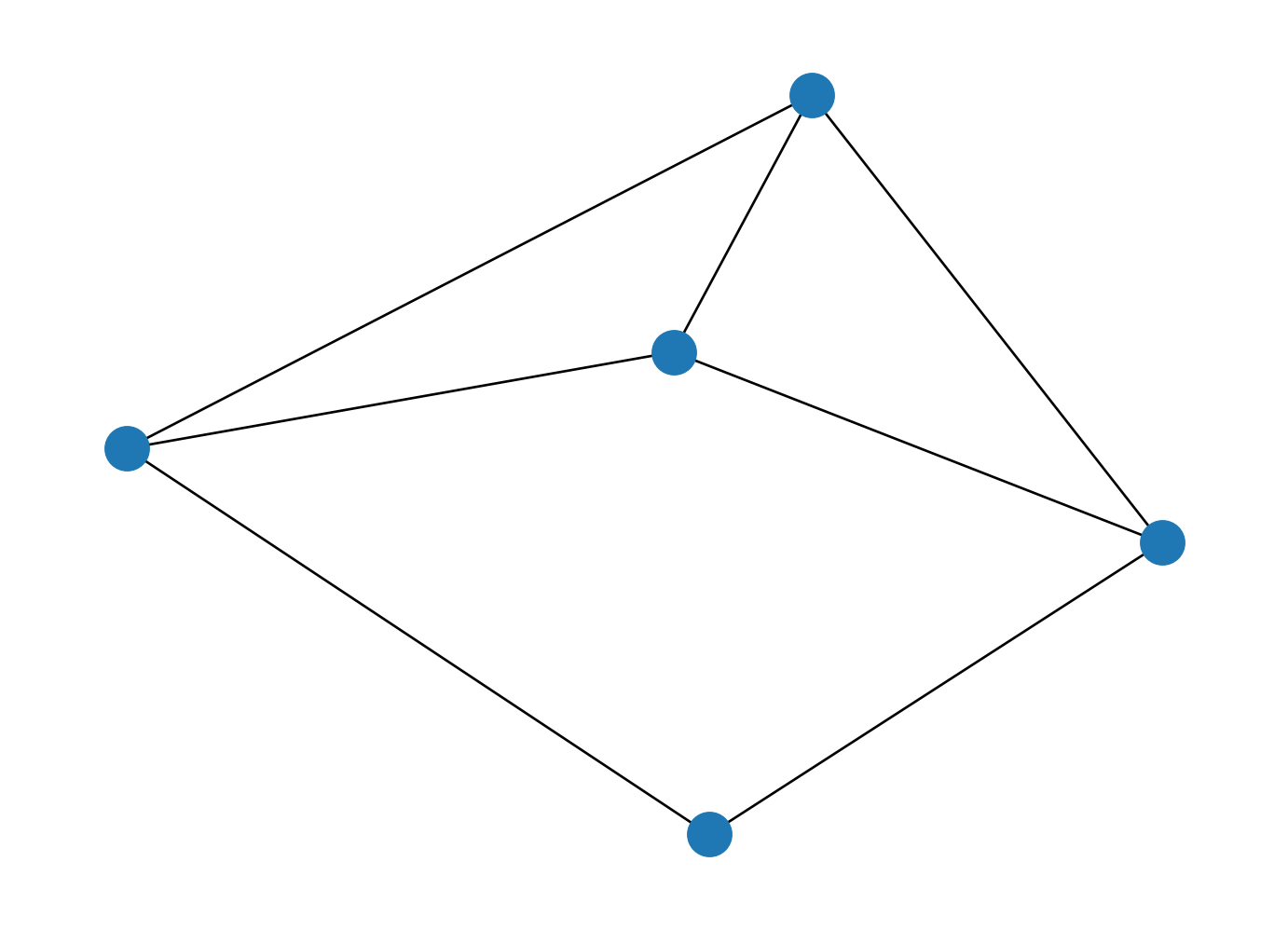
  1. Pour représenter visuellement ce web minimaliste, convertir en objet networkx (une librairie spécialisée dans l’analyse de réseau) et utiliser la fonction draw de ce package.

Il s’agit de la transposée de la matrice d’adjacence qui permet de relier les sites entre eux. Par exemple, le site 1 (première colonne) est référencé par les sites 2 et 3. Celui-ci ne référence que le site 5.

  1. A partir de la page wikipedia anglaise de PageRank, tester sur votre matrice.

Le site 1 est assez central car il est référencé 2 fois. Le site 5 est lui également central puisqu’il est référencé par le site 1.

array([[0.25419178],
       [0.13803151],
       [0.13803151],
       [0.20599017],
       [0.26375504]])

Informations additionnelles

Ce site a été construit automatiquement par le biais d’une action Github utilisant le logiciel de publication reproductible Quarto (version 1.8.26).

L’environnement utilisé pour obtenir les résultats est reproductible par le biais d’uv. Le fichier pyproject.toml utilisé pour construire cet environnement est disponible sur le dépôt linogaliana/python-datascientist

pyproject.toml
[project]
name = "python-datascientist"
version = "0.1.0"
description = "Source code for Lino Galiana's Python for data science course"
readme = "README.md"
requires-python = ">=3.13,<3.14"
dependencies = [
    "altair>=6.0.0",
    "black==24.8.0",
    "cartiflette",
    "contextily==1.6.2",
    "duckdb>=0.10.1",
    "folium>=0.19.6",
    "gdal!=3.11.1",
    "geoplot==0.5.1",
    "graphviz==0.20.3",
    "great-tables>=0.12.0",
    "gt-extras>=0.0.8",
    "ipykernel>=6.29.5",
    "jupyter>=1.1.1",
    "jupyter-cache==1.0.0",
    "kaleido==0.2.1",
    "langchain-community>=0.3.27",
    "loguru==0.7.3",
    "markdown>=3.8",
    "nbclient==0.10.0",
    "nbformat==5.10.4",
    "nltk>=3.9.1",
    "pip>=25.1.1",
    "plotly>=6.1.2",
    "plotnine>=0.15",
    "polars==1.8.2",
    "pyarrow>=17.0.0",
    "pynsee==0.1.8",
    "python-dotenv==1.0.1",
    "python-frontmatter>=1.1.0",
    "pywaffle==1.1.1",
    "requests>=2.32.3",
    "scikit-image==0.24.0",
    "scipy>=1.13.0",
    "selenium<4.39.0",
    "spacy>=3.8.4",
    "webdriver-manager==4.0.2",
    "wordcloud==1.9.3",
]

[tool.uv.sources]
cartiflette = { git = "https://github.com/inseefrlab/cartiflette" }
gdal = [
  { index = "gdal-wheels", marker = "sys_platform == 'linux'" },
  { index = "geospatial_wheels", marker = "sys_platform == 'win32'" },
]

[[tool.uv.index]]
name = "geospatial_wheels"
url = "https://nathanjmcdougall.github.io/geospatial-wheels-index/"
explicit = true

[[tool.uv.index]]
name = "gdal-wheels"
url = "https://gitlab.com/api/v4/projects/61637378/packages/pypi/simple"
explicit = true

[dependency-groups]
dev = [
    "nb-clean>=4.0.1",
]

Pour utiliser exactement le même environnement (version de Python et packages), se reporter à la documentation d’uv.

SHA Date Author Description
5f7df3c4 2026-01-11 21:56:28 Lino Galiana Exercice loi des grands nombres avec Numpy (#673)
ff5f896b 2025-10-03 14:10:58 lgaliana Affiche la correction de l’exo 4 numpy
6d37e77a 2025-09-23 22:58:21 Lino Galiana Correction des problèmes du notebook Pandas (#653)
794ce14a 2025-09-15 16:21:42 lgaliana retouche quelques abstracts
eeb949c8 2025-08-21 17:38:40 Lino Galiana Fix a few problems detected by AI agent (#641)
1884aef7 2025-07-28 13:47:11 lgaliana Teste une extension différente
7006f605 2025-07-28 14:20:47 Lino Galiana Une première PR qui gère plein de bugs détectés par Nicolas (#630)
94648290 2025-07-22 18:57:48 Lino Galiana Fix boxes now that it is better supported by jupyter (#628)
91431fa2 2025-06-09 17:08:00 Lino Galiana Improve homepage hero banner (#612)
488780a4 2024-09-25 14:32:16 Lino Galiana Change badge (#556)
4640e6da 2024-09-18 11:53:05 linogaliana corrections
88b030e8 2024-08-08 17:45:56 Lino Galiana Replace by English metadata when relevant (#535)
580cba77 2024-08-07 18:59:35 Lino Galiana Multilingual version as quarto profile (#533)
72f42bb7 2024-07-25 19:06:38 Lino Galiana Language message on notebooks (#529)
195dc9e9 2024-07-25 11:59:19 linogaliana Switch language button
6bf883d9 2024-07-08 15:09:21 Lino Galiana Rename files (#518)
56b6442d 2024-07-08 15:05:57 Lino Galiana Version anglaise du chapitre numpy (#516)
065b0abd 2024-07-08 11:19:43 Lino Galiana Nouveaux callout dans la partie manipulation (#513)
d75641d7 2024-04-22 18:59:01 Lino Galiana Editorialisation des chapitres de manipulation de données (#491)
005d89b8 2023-12-20 17:23:04 Lino Galiana Finalise l’affichage des statistiques Git (#478)
16842200 2023-12-02 12:06:40 Antoine Palazzolo Première partie de relecture de fin du cours (#467)
1f23de28 2023-12-01 17:25:36 Lino Galiana Stockage des images sur S3 (#466)
a06a2689 2023-11-23 18:23:28 Antoine Palazzolo 2ème relectures chapitres ML (#457)
889a71ba 2023-11-10 11:40:51 Antoine Palazzolo Modification TP 3 (#443)
a7711832 2023-10-09 11:27:45 Antoine Palazzolo Relecture TD2 par Antoine (#418)
a63319ad 2023-10-04 15:29:04 Lino Galiana Correction du TP numpy (#419)
e8d0062d 2023-09-26 15:54:49 Kim A Relecture KA 25/09/2023 (#412)
154f09e4 2023-09-26 14:59:11 Antoine Palazzolo Des typos corrigées par Antoine (#411)
a8f90c2f 2023-08-28 09:26:12 Lino Galiana Update featured paths (#396)
80823022 2023-08-25 17:48:36 Lino Galiana Mise à jour des scripts de construction des notebooks (#395)
3bdf3b06 2023-08-25 11:23:02 Lino Galiana Simplification de la structure 🤓 (#393)
9e1e6e41 2023-07-20 02:27:22 Lino Galiana Change launch script (#379)
130ed717 2023-07-18 19:37:11 Lino Galiana Restructure les titres (#374)
ef28fefd 2023-07-07 08:14:42 Lino Galiana Listing pour la première partie (#369)
f21a24d3 2023-07-02 10:58:15 Lino Galiana Pipeline Quarto & Pages 🚀 (#365)
7e15843a 2023-02-13 18:57:28 Lino Galiana from_numpy_array no longer in networkx 3.0 (#353)
a408cc96 2023-02-01 09:07:27 Lino Galiana Ajoute bouton suggérer modification (#347)
3c880d59 2022-12-27 17:34:59 Lino Galiana Chapitre regex + Change les boites dans plusieurs chapitres (#339)
e2b53ac9 2022-09-28 17:09:31 Lino Galiana Retouche les chapitres pandas (#287)
d068cb6d 2022-09-24 14:58:07 Lino Galiana Corrections avec echo true (#279)
b2d48237 2022-09-21 17:36:29 Lino Galiana Relec KA 21/09 (#273)
a56dd451 2022-09-20 15:27:56 Lino Galiana Fix SSPCloud links (#270)
f10815b5 2022-08-25 16:00:03 Lino Galiana Notebooks should now look more beautiful (#260)
494a85ae 2022-08-05 14:49:56 Lino Galiana Images featured ✨ (#252)
d201e3cd 2022-08-03 15:50:34 Lino Galiana Pimp la homepage ✨ (#249)
1ca1a8a7 2022-05-31 11:44:23 Lino Galiana Retour du chapitre API (#228)
4fc58e52 2022-05-25 18:29:25 Lino Galiana Change deployment on SSP Cloud with new filesystem organization (#227)
12965bac 2022-05-25 15:53:27 Lino Galiana :launch: Bascule vers quarto (#226)
9c71d6e7 2022-03-08 10:34:26 Lino Galiana Plus d’éléments sur S3 (#218)
6777f038 2021-10-29 09:38:09 Lino Galiana Notebooks corrections (#171)
2a8809fb 2021-10-27 12:05:34 Lino Galiana Simplification des hooks pour gagner en flexibilité et clarté (#166)
26ea709d 2021-09-27 19:11:00 Lino Galiana Règle quelques problèmes np (#154)
2fa78c9f 2021-09-27 11:24:19 Lino Galiana Relecture de la partie numpy/pandas (#152)
85ba1194 2021-09-16 11:27:56 Lino Galiana Relectures des TP KA avant 1er cours (#142)
2e4d5862 2021-09-02 12:03:39 Lino Galiana Simplify badges generation (#130)
2f7b52d9 2021-07-20 17:37:03 Lino Galiana Improve notebooks automatic creation (#120)
80877d20 2021-06-28 11:34:24 Lino Galiana Ajout d’un exercice de NLP à partir openfood database (#98)
6729a724 2021-06-22 18:07:05 Lino Galiana Mise à jour badge onyxia (#115)
4cdb759c 2021-05-12 10:37:23 Lino Galiana :sparkles: :star2: Nouveau thème hugo :snake: :fire: (#105)
7f9f97bc 2021-04-30 21:44:04 Lino Galiana 🐳 + 🐍 New workflow (docker 🐳) and new dataset for modelization (2020 🇺🇸 elections) (#99)
0a0d0348 2021-03-26 20:16:22 Lino Galiana Ajout d’une section sur S3 (#97)
6d010fa2 2020-09-29 18:45:34 Lino Galiana Simplifie l’arborescence du site, partie 1 (#57)
66f9f87a 2020-09-24 19:23:04 Lino Galiana Introduction des figures générées par python dans le site (#52)
edca3916 2020-09-21 19:31:02 Lino Galiana Change np.is_nan to np.isnan
f9f00cc0 2020-09-15 21:05:54 Lino Galiana enlève quelques TO DO
4677769b 2020-09-15 18:19:24 Lino Galiana Nettoyage des coquilles pour premiers TP (#37)
d48e68fa 2020-09-08 18:35:07 Lino Galiana Continuer la partie pandas (#13)
913047d3 2020-09-08 14:44:41 Lino Galiana Harmonisation des niveaux de titre (#17)
c452b832 2020-07-28 17:32:06 Lino Galiana TP Numpy (#9)
200b6c1f 2020-07-27 12:50:33 Lino Galiana Encore une coquille
5041b280 2020-07-27 12:44:10 Lino Galiana Une coquille à cause d’un bloc jupyter
e8db4cf0 2020-07-24 12:56:38 Lino Galiana modif des markdown
b24a1fe7 2020-07-23 18:20:09 Lino Galiana Add notebook
4f8f1caa 2020-07-23 18:19:28 Lino Galiana fix typo
434d20e8 2020-07-23 18:18:46 Lino Galiana Essai de yaml header
5ac02efd 2020-07-23 18:05:12 Lino Galiana Essai de md généré avec jupytext
Retour au sommet

Citation

BibTeX
@book{galiana2025,
  author = {Galiana, Lino},
  title = {Python pour la data science},
  date = {2025},
  url = {https://pythonds.linogaliana.fr/},
  doi = {10.5281/zenodo.8229676},
  langid = {fr}
}
Veuillez citer ce travail comme suit :
Galiana, Lino. 2025. Python pour la data science. https://doi.org/10.5281/zenodo.8229676.