Premier pas vers l’industrialisation avec les pipelines scikit

Les pipelines Scikit permettent d’intégrer de manière très flexible un ensemble d’opérations de pre-processing et d’entraînement de modèles dans une chaîne d’opérations. Il s’agit d’une approche particulièrement appropriée pour réduire la difficulté à changer d’algorithme ou pour faciliter la ré-application d’un code à de nouvelles données.

Modélisation
Tutoriel
Auteur·rice

Lino Galiana

Date de publication

2024-11-20

Ce chapitre présente la première application d’une journée de cours que j’ai donné à l’Université Dauphine dans le cadre des PSL Data Week.

Dérouler les _slides_ associées ci-dessous ou [cliquer ici](https://linogaliana.github.io/dauphine-week-data/#/title-slide) pour les afficher en plein écran.

Pour lire les données de manière efficace, nous proposons d’utiliser le package duckdb. Pour l’installer, voici la commande :

!pip install duckdb

1 Pourquoi utiliser les pipelines ?

1.1 Définitions préalables

Ce chapitre nous amènera à explorer plusieurs écosystèmes, pour lesquels on retrouve quelques buzz-words dont voici les définitions :

Terme Définition
DevOps Mouvement en ingénierie informatique et une pratique technique visant à l’unification du développement logiciel (dev) et de l’administration des infrastructures informatiques (ops)
MLOps Ensemble de pratiques qui vise à déployer et maintenir des modèles de machine learning en production de manière fiable et efficace

Ce chapitre fera des références régulières au cours de 3e année de l’ENSAE “Mise en production de projets data science”.

1.2 Objectif

Les chapitres précédents ont permis de montrer des bouts de code épars pour entraîner des modèles ou faire du preprocessing. Cette démarche est intéressante pour tâtonner mais risque d’être coûteuse ultérieurement s’il est nécessaire d’ajouter une étape de preprocessing ou de changer d’algorithme.

Les pipelines sont pensés pour simplifier la mise en production ultérieure d’un modèle de machine learning. Ils sont au coeur de la démarche de MLOps qui est présentée dans le cours de 3e année de l’ENSAE de “Mise en production de projets data science”, qui vise à simplifier la mise en oeuvre opérationnelle de projets utilisant des techniques de machine learning.

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd

1.3 Les pipelines Scikit

Heureusement, Scikit propose un excellent outil pour proposer un cadre général pour créer une chaîne de production machine learning. Il s’agit des pipelines. Ils présentent de nombreux intérêts, parmi lesquels :

  • Ils sont très pratiques et lisibles. On rentre des données en entrée, on n’appelle qu’une seule fois les méthodes fit et predict ce qui permet de s’assurer une gestion cohérente des transformations de variables, par exemple après l’appel d’un StandardScaler ;
  • La modularité rend aisée la mise à jour d’un pipeline et renforce la capacité à le réutiliser ;
  • Ils permettent de facilement chercher les hyperparamètres d’un modèle. Sans pipeline, écrire un code qui fait du tuning d’hyperparamètres peut être pénible. Avec les pipelines, c’est une ligne de code ;
  • La sécurité d’être certain que les étapes de preprocessing sont bien appliquées aux jeux de données désirés avant l’estimation.

2 Comment créer un pipeline

Un pipeline est un enchaînement d’opérations qu’on code en enchainant des pairs (clé, valeur) :

  • la clé est le nom du pipeline, cela peut être utile lorsqu’on va représenter le pipeline sous forme de diagramme acyclique (visualisation DAG) ou qu’on veut afficher des informations sur une étape
  • la valeur représente la transformation à mettre en oeuvre dans le pipeline (c’est-à-dire, à l’exception de la dernière étape, mettre en oeuvre une méthode transform et éventuellement une transformation inverse).
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
from sklearn.decomposition import PCA

estimators = [("reduce_dim", PCA()), ("clf", SVC())]
pipe = Pipeline(estimators)
pipe
Pipeline(steps=[('reduce_dim', PCA()), ('clf', SVC())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Au sein d’une étape de pipeline, les paramètres d’un estimateur sont accessibles avec la notation <estimator>__<parameter>. Cela permet de fixer des valeurs pour les arguments des fonctions scikit qui sont appelées au sein d’un pipeline. C’est cela qui rendra l’approche des pipelines particulièrement utile pour la grid search :

from sklearn.model_selection import GridSearchCV

param_grid = {"reduce_dim__n_components": [2, 5, 10], "clf__C": [0.1, 10, 100]}
grid_search = GridSearchCV(pipe, param_grid=param_grid)
grid_search
GridSearchCV(estimator=Pipeline(steps=[('reduce_dim', PCA()), ('clf', SVC())]),
             param_grid={'clf__C': [0.1, 10, 100],
                         'reduce_dim__n_components': [2, 5, 10]})
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Ces pipelines sont initialisés sans données, il s’agit d’une structure formelle que nous allons ensuite ajuster en entraînant des modèles.

2.1 Données utilisées

Nous allons utiliser les données de transactions immobilières DVF pour chercher la meilleure manière de prédire, sachant les caractéristiques d’un bien, son prix.

Ces données sont mises à disposition sur data.gouv. Néanmoins, le format csv n’étant pas pratique pour importer des jeux de données volumineux, nous proposons de privilégier la version Parquet mise à disposition par Eric Mauvière sur data.gouv. L’approche la plus efficace pour lire ces données est d’utiliser DuckDB afin de lire le fichier, extraire les colonnes d’intérêt puis passer à Pandas (pour en savoir plus sur l’intérêt de DuckDB pour lire des fichiers volumineux, vous pouvez consulter ce post de blog ou celui-ci écrit par Eric Mauvière).

Même si, en soi, les gains de temps sont faibles car DuckDB optimise les requêtes HTTPS nécessaires à l’import des données, nous proposons de télécharger les données pour réduire les besoins de bande passante.

import requests
import os

url = "https://www.data.gouv.fr/fr/datasets/r/56bde1e9-e214-408b-888d-34c57ff005c4"
file_name = "dvf.parquet"

# Check if the file already exists
if not os.path.exists(file_name):
    response = requests.get(url)

    if response.status_code == 200:
        with open(file_name, "wb") as f:
            f.write(response.content)
        print("Téléchargement réussi.")
    else:
        print(f"Échec du téléchargement. Code d'état : {response.status_code}")
else:
    print(f"Le fichier '{file_name}' existe déjà. Aucun téléchargement nécessaire.")

En premier lieu, puisque cela va faciliter les requêtes SQL ultérieures, on crée une vue :

import duckdb

duckdb.sql(f'CREATE OR REPLACE VIEW dvf AS SELECT * FROM read_parquet("dvf.parquet")')

Les données prennent la forme suivante :

duckdb.sql(f"SELECT * FROM dvf LIMIT 5")
┌──────────────────────┬────────────────────┬───┬────────────────┬──────────────────────┬─────────────────┐
│ Identifiant de doc…  │ Reference document │ … │ Nature culture │ Nature culture spe…  │ Surface terrain │
│       varchar        │      varchar       │   │    varchar     │       varchar        │      int64      │
├──────────────────────┼────────────────────┼───┼────────────────┼──────────────────────┼─────────────────┤
│ NULL                 │ NULL               │ … │ NULL           │ NULL                 │            NULL │
│ NULL                 │ NULL               │ … │ S              │ NULL                 │              84 │
│ NULL                 │ NULL               │ … │ S              │ NULL                 │              88 │
│ NULL                 │ NULL               │ … │ NULL           │ NULL                 │            NULL │
│ NULL                 │ NULL               │ … │ T              │ NULL                 │             510 │
├──────────────────────┴────────────────────┴───┴────────────────┴──────────────────────┴─────────────────┤
│ 5 rows                                                                             43 columns (5 shown) │
└─────────────────────────────────────────────────────────────────────────────────────────────────────────┘

Les variables que nous allons conserver sont les suivantes, nous allons les reformater pour la suite de l’exercice.

xvars = [
    "Date mutation",
    "Valeur fonciere",
    "Nombre de lots",
    "Code type local",
    "Nombre pieces principales",
]
xvars = ", ".join([f'"{s}"' for s in xvars])
mutations = duckdb.sql(
    f"""
    SELECT
    date_part('month', "Date mutation") AS month,
    substring("Code postal", 1, 2) AS dep,
    {xvars},
    COLUMNS('Surface Carrez.*')
    FROM dvf
    """
).to_df()

colonnes_surface = mutations.columns[mutations.columns.str.startswith("Surface Carrez")]
mutations.loc[:, colonnes_surface] = (
    mutations.loc[:, colonnes_surface]
    .replace({",": "."}, regex=True)
    .astype(float)
    .fillna(0)
)
mutations.head(2)
month dep Date mutation Valeur fonciere Nombre de lots Code type local Nombre pieces principales Surface Carrez du 1er lot Surface Carrez du 2eme lot Surface Carrez du 3eme lot Surface Carrez du 4eme lot Surface Carrez du 5eme lot
0 1 01 2022-01-03 55000.0 1 2.0 1.0 24.1 0.0 0.0 0.0 0.0
1 1 01 2022-01-03 143000.0 0 NaN NaN 0.0 0.0 0.0 0.0 0.0
Introduire un effet confinement

Si vous travaillez avec les données de 2020, n’oubliez pas d’intégrer l’effet confinement dans vos modèles puisque cela a lourdement affecté les possibilités de transaction sur cette période, donc l’effet potentiel de certaines variables explicatives du prix.

Pour introduire cet effet, vous pouvez créer une variable indicatrice entre les dates en question:

mutations["confinement"] = (
    mutations["Date mutation"]
    .between(pd.to_datetime("2020-03-17"), pd.to_datetime("2020-05-03"))
    .astype(int)
)

Comme nous travaillons sur les données de 2022, nous pouvons nous passer de cette variable.

Les données DVF proposent une observation par transaction. Ces transactions peuvent concerner plusieurs lots. Par exemple, un appartement avec garage et cave comportera trois lots.

Pour simplifier, on va créer une variable de surface qui agrège les différentes informations de surface disponibles dans le jeu de données. Les agréger revient à supposer que le modèle de fixation des prix est le même entre chaque lot. C’est une hypothèse simplificatrice qu’une personne plus experte du marché immobilier, ou qu’une approche propre de sélection de variable pourrait amener à nier. En effet, les variables en question sont faiblement corrélées les unes entre elles, à quelques exceptions près (Figure 2.1):

corr = mutations.loc[
    :, mutations.columns[mutations.columns.str.startswith("Surface Carrez")].tolist()
]
corr.columns = corr.columns.str.replace("Carrez du ", "")
corr = corr.corr()

mask = np.triu(np.ones_like(corr, dtype=bool))

cmap = sns.diverging_palette(230, 20, as_cmap=True)
fig, ax = plt.subplots(1)
g = sns.heatmap(
    corr,
    ax=ax,
    mask=mask,
    vmax=0.3,
    center=0,
    square=True,
    linewidths=0.5,
    cbar_kws={"shrink": 0.5},
    xticklabels=corr.columns.values,
    yticklabels=corr.columns.values,
    cmap=cmap,
    annot=True,
    fmt=".2f",
)
g
Figure 2.1: Matrice de corrélation des variables de surface 
mutations["lprix"] = np.log(mutations["Valeur fonciere"])
mutations["surface"] = mutations.loc[:, colonnes_surface].sum(axis=1).astype(int)
/opt/conda/lib/python3.12/site-packages/pandas/core/arraylike.py:399: RuntimeWarning:

divide by zero encountered in log

mutations["surface"] = mutations.loc[
    :, mutations.columns[mutations.columns.str.startswith("Surface Carrez")].tolist()
].sum(axis=1)

3 Un premier pipeline : random forest sur des variables standardisées

Notre premier pipeline va nous permettre d’intégrer ensemble:

  1. Une étape de preprocessing avec la standardisation de variables
  2. Une étape d’estimation du prix en utilisant un modèle de random forest

Pour le moment, on va prendre comme acquis un certain nombre de variables explicatives (les features) et les hyperparamètres du modèle.

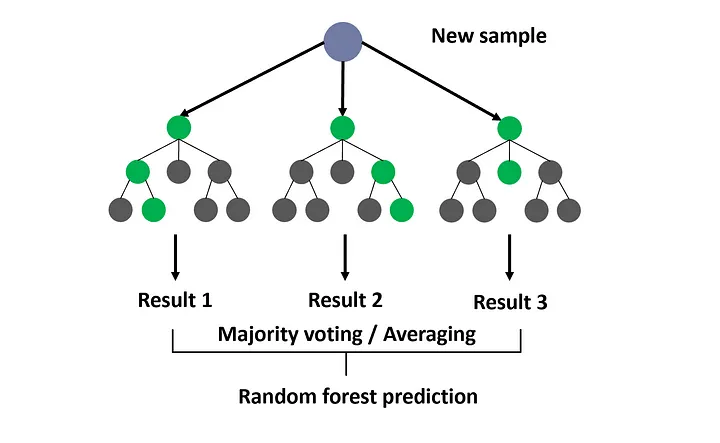
L’algorithme des random forest est une technique statistique basée sur les arbres de décision. Elle a été définie explicitement par l’un des pionniers du machine learning, Breiman (2001). Il s’agit d’une méthode ensembliste puisqu’elle consiste à utiliser plusieurs algorithmes (en l’occurrence des arbres de décision) pour obtenir une meilleure prédiction que ne le permettraient chaque modèle isolément.

Les random forest sont une méthode d’aggrégation1 d’arbres de décision. On calcule \(K\) arbres de décision et en tire, par une méthode d’agrégation, une règle de décision moyenne qu’on va appliquer pour tirer une prédiction de nos données.

L’un des intérêts des random forest est qu’il existe des méthodes pour déterminer l’importance relative de chaque variable dans la prédiction.

Nous allons ici partir d’un random forest avec des valeurs d’hyperparamètres données, à savoir la profondeur de l’arbre.

3.1 Définition des ensembles train et test

Nous allons donc nous restreindre à un sous-ensemble de colonnes dans un premier temps.

Nous allons également ne conserver que les transactions inférieures à 5 millions d’euros (on anticipe que celles ayant un montant supérieur sont des transactions exceptionnelles dont le mécanisme de fixation du prix diffère)

mutations2 = mutations.drop(
    colonnes_surface.tolist()
    + ["Date mutation", "lprix"],  # ajouter "confinement" si données 2020
    axis="columns",
).copy()

mutations2 = mutations2.loc[
    mutations2["Valeur fonciere"] < 5e6
]  # keep only values below 5 millions

mutations2.columns = mutations2.columns.str.replace(" ", "_")
mutations2 = mutations2.dropna(subset=["dep", "Code_type_local", "month"])

Notre pipeline va incorporer deux types de variables: les variables catégorielles et les variables numériques. Ces différents types vont bénéficier d’étapes de preprocessing différentes.

numeric_features = mutations2.columns[
    ~mutations2.columns.isin(["dep", "Code_type_local", "month", "Valeur_fonciere"])
].tolist()
categorical_features = ["dep", "Code_type_local", "month"]

Au passage, nous avons abandonné la variable de code postal pour privilégier le département afin de réduire la dimension de notre jeu de données. Si on voulait vraiment avoir un bon modèle, il faudrait faire autrement car le code postal est probablement un très bon prédicteur du prix d’un bien, une fois que les caractéristiques du bien sont contrôlées.

3.2 Définition du premier pipeline

Pour commencer, nous allons fixer la taille des arbres de décision avec l’hyperparamètre max_depth = 2.

Notre pipeline va intégrer les étapes suivantes :

  1. Preprocessing :
    • Les variables numériques vont être standardisées avec un StandardScaler. Pour cela, nous allons utiliser la liste numeric_features définie précédemment.
    • Les variables catégorielles vont être explosées avec un one hot encoding (méthode OneHotEncoder de scikit) Pour cela, nous allons utiliser la liste categorical_features
  2. Random forest : nous allons appliquer l’estimateur ad hoc de Scikit.

A l’issue de cet exercice, nous devrions obtenir le pipeline suivant.

Pipeline(steps=[('preprocessor',
                 ColumnTransformer(transformers=[('pipeline',
                                                  Pipeline(steps=[('simpleimputer',
                                                                   SimpleImputer()),
                                                                  ('standardscaler',
                                                                   StandardScaler())]),
                                                  ['Nombre_de_lots',
                                                   'Nombre_pieces_principales',
                                                   'surface']),
                                                 ('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore',
                                                                sparse_output=False),
                                                  ['dep', 'Code_type_local',
                                                   'month'])])),
                ('randomforest',
                 RandomForestRegressor(max_depth=2, random_state=123))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Nous avons construit ce pipeline sous forme de couches successives. La couche randomforest prendra automatiquement le résultat de la couche preprocessor en input. La couche features permet d’introduire de manière relativement simple (quand on a les bonnes méthodes) la complexité du preprocessing sur données réelles dont les types divergent.

A cette étape, rien n’a encore été estimé. C’est très simple à mettre en oeuvre avec un pipeline.

Pipeline(steps=[('preprocessor',
                 ColumnTransformer(transformers=[('pipeline',
                                                  Pipeline(steps=[('simpleimputer',
                                                                   SimpleImputer()),
                                                                  ('standardscaler',
                                                                   StandardScaler())]),
                                                  ['Nombre_de_lots',
                                                   'Nombre_pieces_principales',
                                                   'surface']),
                                                 ('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore',
                                                                sparse_output=False),
                                                  ['dep', 'Code_type_local',
                                                   'month'])])),
                ('randomforest',
                 RandomForestRegressor(max_depth=2, random_state=123))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
array([282871.63598981, 301165.65351098, 301165.65351098, ...,
       282871.63598981, 471048.40037679, 282871.63598981])
array([642280.20111587, 282871.63598981])
433497.6437239088

3.3 Variable importance

Les prédictions semblent avoir une assez faible variance, comme si des variables de seuils intervenaient. Nous allons donc devoir essayer de comprendre pourquoi.

La “variable importance” se réfère à la mesure de l’influence de chaque variable d’entrée sur la performance du modèle. L’impureté fait référence à l’incertitude ou à l’entropie présente dans un ensemble de données. Dans le contexte des random forest, cette mesure est souvent calculée en évaluant la réduction moyenne de l’impureté des nœuds de décision causée par une variable spécifique. Cette approche permet de quantifier l’importance des variables dans le processus de prise de décision du modèle, offrant ainsi des intuitions sur les caractéristiques les plus informatives pour la prédiction (plus de détails sur ce blog).

On ne va représenter, parmi notre ensemble important de colonnes, que celles qui ont une importance non nulle.

Le graphique d’importance des variables que vous devriez obtenir à l’issue de cet exercice est le suivant.

<Axes: title={'center': 'Feature importances using MDI'}, ylabel='Mean decrease in impurity'>

Les statistiques obtenues par le biais de cette variable importance sont un peu rudimentaires mais permettent déjà de comprendre le problème de notre modèle.

On voit donc que deux de nos variables déterminantes sont des effets fixes géographiques (qui servent à ajuster de la différence de prix entre Paris et les Hauts de Seine et le reste de la France), une autre variable est un effet fixe type de bien. Les deux variables qui pourraient introduire de la variabilité, à savoir la surface et, dans une moindre mesure, le nombre de lots, ont une importance moindre.

Les prédictions peuvent nous suggérer également qu’il y a un problème.

4 Restriction du champ du modèle

Mettre en oeuvre un bon modèle de prix au niveau France entière est complexe. Nous allons donc nous restreindre au champ suivant: les appartements dans Paris.

mutations_paris = mutations.drop(
    colonnes_surface.tolist()
    + ["Date mutation", "lprix"],  # ajouter "confinement" si données 2020
    axis="columns",
).copy()

mutations_paris = mutations_paris.loc[
    mutations_paris["Valeur fonciere"] < 5e6
]  # keep only values below 5 millions

mutations_paris.columns = mutations_paris.columns.str.replace(" ", "_")
mutations_paris = mutations_paris.dropna(subset=["dep", "Code_type_local", "month"])
mutations_paris = mutations_paris.loc[mutations_paris["dep"] == "75"]
mutations_paris = mutations_paris.loc[mutations_paris["Code_type_local"] == 2].drop(
    ["dep", "Code_type_local"], axis="columns"
)
mutations_paris.loc[mutations_paris["surface"] > 0]
month Valeur_fonciere Nombre_de_lots Nombre_pieces_principales surface
4272176 1 686000.0 1 4.0 73.45
4273807 2 400000.0 1 2.0 41.16
4275450 3 475000.0 3 2.0 47.7
4275883 2 396200.0 2 2.0 47.14
4275884 2 299500.0 1 1.0 34.02
... ... ... ... ... ...
4617521 12 1650000.0 3 6.0 154.75
4617532 12 525000.0 2 3.0 46.65
4617540 12 425000.0 2 1.0 27.85
4617549 12 330000.0 2 2.0 34.32
4617577 3 232650.0 1 1.0 28.25

27971 rows × 5 columns

A l’issue de cet exercice, vous devriez avoir des MDI proches de celles-ci :

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.pipeline import make_pipeline, Pipeline
from sklearn.compose import make_column_transformer
from sklearn.model_selection import train_test_split


mutations_paris = mutations.drop(
    colonnes_surface.tolist()
    + ["Date mutation", "lprix"],  # ajouter "confinement" si données 2020
    axis="columns",
).copy()

mutations_paris = mutations_paris.loc[
    mutations_paris["Valeur fonciere"] < 5e6
]  # keep only values below 5 millions

mutations_paris.columns = mutations_paris.columns.str.replace(" ", "_")
mutations_paris = mutations_paris.dropna(subset=["dep", "Code_type_local", "month"])
mutations_paris = mutations_paris.loc[mutations_paris["dep"] == "75"]
mutations_paris = mutations_paris.loc[mutations_paris["Code_type_local"] == 2].drop(
    ["dep", "Code_type_local", "Nombre_de_lots"], axis="columns"
)
mutations_paris.loc[mutations_paris["surface"] > 0]


numeric_features = mutations_paris.columns[
    ~mutations_paris.columns.isin(["month", "Valeur_fonciere"])
].tolist()
categorical_features = ["month"]

reg = GradientBoostingRegressor(random_state=0)

numeric_pipeline = make_pipeline(SimpleImputer(), StandardScaler())
transformer = make_column_transformer(
    (numeric_pipeline, numeric_features),
    (OneHotEncoder(sparse_output=False, handle_unknown="ignore"), categorical_features),
)
pipe = Pipeline(steps=[("preprocessor", transformer), ("boosting", reg)])

X_train, X_test, y_train, y_test = train_test_split(
    mutations_paris.drop("Valeur_fonciere", axis=1),
    mutations_paris[["Valeur_fonciere"]].values.ravel(),
    test_size=0.2,
    random_state=123,
)

pipe.fit(X_train, y_train)

pd.DataFrame(
    pipe["boosting"].feature_importances_, index=pipe[:-1].get_feature_names_out()
)
0
pipeline__Nombre_pieces_principales 0.268176
pipeline__surface 0.716371
onehotencoder__month_1 0.000309
onehotencoder__month_2 0.001060
onehotencoder__month_3 0.000967
onehotencoder__month_4 0.007498
onehotencoder__month_5 0.000000
onehotencoder__month_6 0.000153
onehotencoder__month_7 0.000156
onehotencoder__month_8 0.000819
onehotencoder__month_9 0.000026
onehotencoder__month_10 0.002170
onehotencoder__month_11 0.001690
onehotencoder__month_12 0.000605

5 Recherche des hyperparamètres optimaux avec une validation croisée

On détecte que le premier modèle n’est pas très bon et ne nous aidera pas vraiment à évaluer de manière fiable l’appartement de nos rêves.

On va essayer de voir si notre modèle ne serait pas meilleur avec des hyperparamètres plus adaptés. Après tout, nous avons choisi par défaut la profondeur de l’arbre mais c’était un choix au doigt mouillé.

❓️ Quels sont les hyperparamètres qu’on peut essayer d’optimiser ?

pipe["boosting"].get_params()
{'alpha': 0.9,
 'ccp_alpha': 0.0,
 'criterion': 'friedman_mse',
 'init': None,
 'learning_rate': 0.1,
 'loss': 'squared_error',
 'max_depth': 3,
 'max_features': None,
 'max_leaf_nodes': None,
 'min_impurity_decrease': 0.0,
 'min_samples_leaf': 1,
 'min_samples_split': 2,
 'min_weight_fraction_leaf': 0.0,
 'n_estimators': 100,
 'n_iter_no_change': None,
 'random_state': 0,
 'subsample': 1.0,
 'tol': 0.0001,
 'validation_fraction': 0.1,
 'verbose': 0,
 'warm_start': False}

Un détour par la documentation nous aide à comprendre ceux sur lesquels on va jouer. Par exemple, il serait absurde de jouer sur le paramètre random_state qui est la racine du générateur pseudo-aléatoire.

X = pd.concat((X_train, X_test), axis=0)
Y = np.concatenate([y_train, y_test])

Nous allons nous contenter de jouer sur les paramètres:

  • n_estimators: Le nombre d’arbres de décision que notre forêt contient
  • max_depth: La profondeur de chaque arbre

Il existe plusieurs manières de faire de la validation croisée. Nous allons ici utiliser la grid search qui consiste à estimer et tester le modèle sur chaque combinaison d’une grille de paramètres et sélectionner le couple de valeurs des hyperparamètres amenant à la meilleure prédiction. Par défaut, scikit effectue une 5-fold cross validation. Nous n’allons pas changer ce comportement.

Comme expliqué précédemment, les paramètres s’appelent sous la forme <step>__<parameter_name>

La validation croisée pouvant être très consommatrice de temps, nous n’allons l’effectuer que sur un nombre réduit de valeurs de notre grille. Il est possible de passer la liste des valeurs à passer au crible sous forme de liste (comme nous allons le proposer pour l’argument max_depth dans l’exercice ci-dessous) ou sous forme d’array (comme nous allons le proposer pour l’argument n_estimators) ce qui est souvent pratique pour générer un criblage d’un intervalle avec np.linspace.

GridSearchCV(estimator=Pipeline(steps=[('preprocessor',
                                        ColumnTransformer(transformers=[('pipeline',
                                                                         Pipeline(steps=[('simpleimputer',
                                                                                          SimpleImputer()),
                                                                                         ('standardscaler',
                                                                                          StandardScaler())]),
                                                                         ['Nombre_pieces_principales',
                                                                          'surface']),
                                                                        ('onehotencoder',
                                                                         OneHotEncoder(handle_unknown='ignore',
                                                                                       sparse_output=False),
                                                                         ['month'])])),
                                       ('boosting',
                                        GradientBoostingRegressor(random_state=0))]),
             param_grid={'boosting__max_depth': [2, 4],
                         'boosting__n_estimators': array([ 5, 10, 15, 20, 25])})
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
grid_search.best_params_
grid_search.best_estimator_
Pipeline(steps=[('preprocessor',
                 ColumnTransformer(transformers=[('pipeline',
                                                  Pipeline(steps=[('simpleimputer',
                                                                   SimpleImputer()),
                                                                  ('standardscaler',
                                                                   StandardScaler())]),
                                                  ['Nombre_pieces_principales',
                                                   'surface']),
                                                 ('onehotencoder',
                                                  OneHotEncoder(handle_unknown='ignore',
                                                                sparse_output=False),
                                                  ['month'])])),
                ('boosting',
                 GradientBoostingRegressor(max_depth=4, n_estimators=25,
                                           random_state=0))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Toutes les performances sur les ensembles d’échantillons et de test sur la grille d’hyperparamètres sont disponibles dans l’attribut:

perf_random_forest = pd.DataFrame(grid_search.cv_results_)

Regardons les résultats moyens pour chaque valeur des hyperparamètres:

fig, ax = plt.subplots(1)
g = sns.lineplot(
    data=perf_random_forest,
    ax=ax,
    x="param_boosting__n_estimators",
    y="mean_test_score",
    hue="param_boosting__max_depth",
)
g.set(xlabel="Number of estimators", ylabel="Mean score on test sample")
g
plt.legend(
    bbox_to_anchor=(1.05, 1), loc="upper left", borderaxespad=0, title="Depth of trees"
)

Globalement, à profondeur d’arbre donnée, le nombre d’arbres affecte la performance. Changer la profondeur de l’arbre améliore la performance de manière plus marquée.

Maintenant, il nous reste à re-entraîner le modèle avec ces nouveaux paramètres sur l’ensemble du jeu de train et l’évaluer sur l’ensemble du jeu de test :

pipe_optimal = grid_search.best_estimator_
pipe_optimal.fit(X_train, y_train)

compar = pd.DataFrame([y_test, pipe_optimal.predict(X_test)]).T
compar.columns = ["obs", "pred"]
compar["diff"] = compar.obs - compar.pred

On obtient le RMSE suivant :

Le RMSE sur le jeu de test est 562,317

Et si on regarde la qualité en prédiction:

On obtient plus de variance dans la prédiction, c’est déjà un peu mieux. Cependant, cela reste décevant pour plusieurs raisons:

  • nous n’avons pas fait d’étape de sélection de variable
  • nous n’avons pas chercher à déterminer si la variable à prédire la plus pertinente était le prix ou une transformation de celle-ci (par exemple le prix au \(m^2\))

6 Prochaine étape

Nous avons un modèle certes perfectible mais fonctionnel. La question qui se pose maintenant c’est d’essayer d’en faire quelque chose au service des utilisateurs. Cela nous amène vers la question de la mise en production.

Ceci est l’objet du prochain chapitre. Il s’agira d’une version introductive des enjeux évoqués dans le cadre du cours de 3e année de mise en production de projets de data science.

7 Références

Informations additionnelles

environment files have been tested on.

Latest built version: 2024-11-20

Python version used:

'3.12.6 | packaged by conda-forge | (main, Sep 30 2024, 18:08:52) [GCC 13.3.0]'
Package Version
affine 2.4.0
aiobotocore 2.15.1
aiohappyeyeballs 2.4.3
aiohttp 3.10.8
aioitertools 0.12.0
aiosignal 1.3.1
alembic 1.13.3
altair 5.4.1
aniso8601 9.0.1
annotated-types 0.7.0
appdirs 1.4.4
archspec 0.2.3
asttokens 2.4.1
attrs 24.2.0
babel 2.16.0
bcrypt 4.2.0
beautifulsoup4 4.12.3
black 24.8.0
blinker 1.8.2
blis 0.7.11
bokeh 3.5.2
boltons 24.0.0
boto3 1.35.23
botocore 1.35.23
branca 0.7.2
Brotli 1.1.0
bs4 0.0.2
cachetools 5.5.0
cartiflette 0.0.2
Cartopy 0.24.1
catalogue 2.0.10
cattrs 24.1.2
certifi 2024.8.30
cffi 1.17.1
charset-normalizer 3.3.2
chromedriver-autoinstaller 0.6.4
click 8.1.7
click-plugins 1.1.1
cligj 0.7.2
cloudpathlib 0.20.0
cloudpickle 3.0.0
colorama 0.4.6
comm 0.2.2
commonmark 0.9.1
conda 24.9.1
conda-libmamba-solver 24.7.0
conda-package-handling 2.3.0
conda_package_streaming 0.10.0
confection 0.1.5
contextily 1.6.2
contourpy 1.3.0
cryptography 43.0.1
cycler 0.12.1
cymem 2.0.8
cytoolz 1.0.0
dask 2024.9.1
dask-expr 1.1.15
databricks-sdk 0.33.0
debugpy 1.8.6
decorator 5.1.1
Deprecated 1.2.14
diskcache 5.6.3
distributed 2024.9.1
distro 1.9.0
docker 7.1.0
duckdb 0.10.1
en-core-web-sm 3.7.1
entrypoints 0.4
et_xmlfile 2.0.0
exceptiongroup 1.2.2
executing 2.1.0
fastexcel 0.11.6
fastjsonschema 2.20.0
fiona 1.10.1
Flask 3.0.3
folium 0.17.0
fontawesomefree 6.6.0
fonttools 4.54.1
fr-core-news-sm 3.7.0
frozendict 2.4.4
frozenlist 1.4.1
fsspec 2023.12.2
funcy 2.0
gensim 4.3.2
geographiclib 2.0
geopandas 1.0.1
geoplot 0.5.1
geopy 2.4.1
gitdb 4.0.11
GitPython 3.1.43
google-auth 2.35.0
graphene 3.3
graphql-core 3.2.4
graphql-relay 3.2.0
graphviz 0.20.3
great-tables 0.12.0
greenlet 3.1.1
gunicorn 22.0.0
h11 0.14.0
h2 4.1.0
hpack 4.0.0
htmltools 0.6.0
hyperframe 6.0.1
idna 3.10
imageio 2.36.0
importlib_metadata 8.5.0
importlib_resources 6.4.5
inflate64 1.0.0
ipykernel 6.29.5
ipython 8.28.0
itsdangerous 2.2.0
jedi 0.19.1
Jinja2 3.1.4
jmespath 1.0.1
joblib 1.4.2
jsonpatch 1.33
jsonpointer 3.0.0
jsonschema 4.23.0
jsonschema-specifications 2024.10.1
jupyter-cache 1.0.0
jupyter_client 8.6.3
jupyter_core 5.7.2
kaleido 0.2.1
kiwisolver 1.4.7
langcodes 3.5.0
language_data 1.3.0
lazy_loader 0.4
libmambapy 1.5.9
locket 1.0.0
lxml 5.3.0
lz4 4.3.3
Mako 1.3.5
mamba 1.5.9
mapclassify 2.8.1
marisa-trie 1.2.1
Markdown 3.6
markdown-it-py 3.0.0
MarkupSafe 2.1.5
matplotlib 3.9.2
matplotlib-inline 0.1.7
mdurl 0.1.2
menuinst 2.1.2
mercantile 1.2.1
mizani 0.11.4
mlflow 2.16.2
mlflow-skinny 2.16.2
msgpack 1.1.0
multidict 6.1.0
multivolumefile 0.2.3
munkres 1.1.4
murmurhash 1.0.10
mypy-extensions 1.0.0
narwhals 1.14.1
nbclient 0.10.0
nbformat 5.10.4
nest_asyncio 1.6.0
networkx 3.3
nltk 3.9.1
numexpr 2.10.1
numpy 1.26.4
opencv-python-headless 4.10.0.84
openpyxl 3.1.5
opentelemetry-api 1.16.0
opentelemetry-sdk 1.16.0
opentelemetry-semantic-conventions 0.37b0
outcome 1.3.0.post0
OWSLib 0.28.1
packaging 24.1
pandas 2.2.3
paramiko 3.5.0
parso 0.8.4
partd 1.4.2
pathspec 0.12.1
patsy 0.5.6
Pebble 5.0.7
pexpect 4.9.0
pickleshare 0.7.5
pillow 10.4.0
pip 24.2
platformdirs 4.3.6
plotly 5.24.1
plotnine 0.13.6
pluggy 1.5.0
polars 1.8.2
preshed 3.0.9
prometheus_client 0.21.0
prometheus_flask_exporter 0.23.1
prompt_toolkit 3.0.48
protobuf 4.25.3
psutil 6.0.0
ptyprocess 0.7.0
pure_eval 0.2.3
py7zr 0.20.8
pyarrow 17.0.0
pyarrow-hotfix 0.6
pyasn1 0.6.1
pyasn1_modules 0.4.1
pybcj 1.0.2
pycosat 0.6.6
pycparser 2.22
pycryptodomex 3.21.0
pydantic 2.9.2
pydantic_core 2.23.4
Pygments 2.18.0
pyLDAvis 3.4.1
PyNaCl 1.5.0
pynsee 0.1.8
pyogrio 0.10.0
pyOpenSSL 24.2.1
pyparsing 3.1.4
pyppmd 1.1.0
pyproj 3.7.0
pyshp 2.3.1
PySocks 1.7.1
python-dateutil 2.9.0
python-dotenv 1.0.1
python-magic 0.4.27
pytz 2024.1
pyu2f 0.1.5
pywaffle 1.1.1
PyYAML 6.0.2
pyzmq 26.2.0
pyzstd 0.16.2
querystring_parser 1.2.4
rasterio 1.4.2
referencing 0.35.1
regex 2024.9.11
requests 2.32.3
requests-cache 1.2.1
retrying 1.3.4
rich 13.9.4
rpds-py 0.21.0
rsa 4.9
Rtree 1.3.0
ruamel.yaml 0.18.6
ruamel.yaml.clib 0.2.8
s3fs 2023.12.2
s3transfer 0.10.2
scikit-image 0.24.0
scikit-learn 1.5.2
scipy 1.13.0
seaborn 0.13.2
selenium 4.26.1
setuptools 74.1.2
shapely 2.0.6
shellingham 1.5.4
six 1.16.0
smart-open 7.0.5
smmap 5.0.0
sniffio 1.3.1
sortedcontainers 2.4.0
soupsieve 2.5
spacy 3.7.5
spacy-legacy 3.0.12
spacy-loggers 1.0.5
SQLAlchemy 2.0.35
sqlparse 0.5.1
srsly 2.4.8
stack-data 0.6.2
statsmodels 0.14.4
tabulate 0.9.0
tblib 3.0.0
tenacity 9.0.0
texttable 1.7.0
thinc 8.2.5
threadpoolctl 3.5.0
tifffile 2024.9.20
toolz 1.0.0
topojson 1.9
tornado 6.4.1
tqdm 4.66.5
traitlets 5.14.3
trio 0.27.0
trio-websocket 0.11.1
truststore 0.9.2
typer 0.13.1
typing_extensions 4.12.2
tzdata 2024.2
Unidecode 1.3.8
url-normalize 1.4.3
urllib3 1.26.20
wasabi 1.1.3
wcwidth 0.2.13
weasel 0.4.1
webdriver-manager 4.0.2
websocket-client 1.8.0
Werkzeug 3.0.4
wheel 0.44.0
wordcloud 1.9.3
wrapt 1.16.0
wsproto 1.2.0
xgboost 2.1.1
xlrd 2.0.1
xyzservices 2024.9.0
yarl 1.13.1
yellowbrick 1.5
zict 3.0.0
zipp 3.20.2
zstandard 0.23.0

View file history

SHA Date Author Description
d242257 2024-08-22 18:51:51 Lino Galiana At this point, notebooks should now all be functional ! (#547)
c641de0 2024-08-22 11:37:13 Lino Galiana A series of fix for notebooks that were bugging (#545)
0908656 2024-08-20 16:30:39 Lino Galiana English sidebar (#542)
8f0d2e1 2024-05-07 15:06:45 lgaliana Duplicate data from datagouv
c9f9f8a 2024-04-24 15:09:35 Lino Galiana Dark mode and CSS improvements (#494)
06d003a 2024-04-23 10:09:22 Lino Galiana Continue la restructuration des sous-parties (#492)
8c316d0 2024-04-05 19:00:59 Lino Galiana Fix cartiflette deprecated snippets (#487)
005d89b 2023-12-20 17:23:04 Lino Galiana Finalise l’affichage des statistiques Git (#478)
3fba612 2023-12-17 18:16:42 Lino Galiana Remove some badges from python (#476)
4cd44f3 2023-12-11 17:37:50 Antoine Palazzolo Relecture NLP (#474)
1684220 2023-12-02 12:06:40 Antoine Palazzolo Première partie de relecture de fin du cours (#467)
e4642ee 2023-11-27 17:02:05 Lino Galiana Deploy ML model as API (#460)
a06a268 2023-11-23 18:23:28 Antoine Palazzolo 2ème relectures chapitres ML (#457)
4960f2b 2023-11-22 12:02:32 Lino Galiana Chapitre pipeline scikit sur DVF (#454)
69cf52b 2023-11-21 16:12:37 Antoine Palazzolo [On-going] Suggestions chapitres modélisation (#452)
889a71b 2023-11-10 11:40:51 Antoine Palazzolo Modification TP 3 (#443)
652009d 2023-10-09 13:56:34 Lino Galiana Finalise le cleaning (#430)
a771183 2023-10-09 11:27:45 Antoine Palazzolo Relecture TD2 par Antoine (#418)
154f09e 2023-09-26 14:59:11 Antoine Palazzolo Des typos corrigées par Antoine (#411)
3bdf3b0 2023-08-25 11:23:02 Lino Galiana Simplification de la structure 🤓 (#393)
78ea2cb 2023-07-20 20:27:31 Lino Galiana Change titles levels (#381)
29ff3f5 2023-07-07 14:17:53 linogaliana description everywhere
f21a24d 2023-07-02 10:58:15 Lino Galiana Pipeline Quarto & Pages 🚀 (#365)
38693f6 2023-04-19 17:22:36 Lino Galiana Rebuild visualisation part (#357)
3248633 2023-02-18 13:11:52 Lino Galiana Shortcode rawhtml (#354)
f10815b 2022-08-25 16:00:03 Lino Galiana Notebooks should now look more beautiful (#260)
494a85a 2022-08-05 14:49:56 Lino Galiana Images featured ✨ (#252)
d201e3c 2022-08-03 15:50:34 Lino Galiana Pimp la homepage ✨ (#249)
12965ba 2022-05-25 15:53:27 Lino Galiana :launch: Bascule vers quarto (#226)
9c71d6e 2022-03-08 10:34:26 Lino Galiana Plus d’éléments sur S3 (#218)
ed2ddec 2022-01-04 13:32:43 Expressso retire typo (#212)
66e2837 2021-12-24 16:54:45 Lino Galiana Fix a few typos in the new pipeline tutorial (#208)
e94c1c5 2021-12-23 21:34:46 Lino Galiana Un tutoriel sur les pipelines :tada: (#203)
Retour au sommet

Les références

Breiman, Leo. 1996. « Bagging predictors ». Machine learning 24: 123‑40.
———. 2001. « Random forests ». Machine learning 45: 5‑32.

Notes de bas de page

  1. Les random forest sont l’une des principales méthodes ensemblistes. Outre cette approche, les plus connues sont le bagging (boostrap aggregating) et le boosting qui consistent à choisir la prédiction à privilégier selon des algorithmes de choix différens. Par exemple le bagging est une technique basée sur le vote majoritaire (Breiman 1996). Cette technique s’inspire du bootstrap qui, en économétrie, consiste à ré-estimer sur K sous-échantillons aléatoires des données un estimateur afin d’en tirer, par exemple, un intervalle de confiance empirique à 95%. Le principe du bagging est le même. On ré-estime K fois notre estimateur (par exemple un arbre de décision) et propose une règle d’agrégation pour en tirer une règle moyennisée et donc une prédiction. Le boosting fonctionne selon un principe différent, basé sur l’optimisation de combinaisons de classifieurs faibles.↩︎

Citation

BibTeX
@book{galiana2023,
  author = {Galiana, Lino},
  title = {Python pour la data science},
  date = {2023},
  url = {https://pythonds.linogaliana.fr/},
  doi = {10.5281/zenodo.8229676},
  langid = {fr}
}
Veuillez citer ce travail comme suit :
Galiana, Lino. 2023. Python pour la data science. https://doi.org/10.5281/zenodo.8229676.