!pip install pandas fiona shapely pyproj rtree
!pip install contextily
!pip install geopandas
!pip install topojsonPour essayer les exemples présents dans ce tutoriel :
1 Introduction
1.1 Quelle différence avec des données traditionnelles ?
Les chapitres précédents ont permis de découvrir la manière
dont des données structurées peuvent être valorisées
grâce à la librairie Pandas. Nous allons maintenant découvrir l’analyse
de données plus complexes, à savoir les données spatiales.
Ces
dernières sont une sophistication des données tabulaires puisqu’en plus
de partager les propriétés de celles-ci (données aplaties dans une structure de colonnes et de lignes), elles comportent une dimension géographique supplémentaire. Celle-ci est plus ou moins complexe selon la nature des données: cela peut être des points (coordonnées de localisation en deux dimensions), des lignes (une suite de points), des lignes directionnelles (la même structure précédemment mais avec une direction), des polygones (un ensemble de points)… Cette diversité des objets géographiques vise à permettre des systèmes d’information et de représentation de nombreux objets géographiques.
Par la suite, nous entendrons par “données spatiales” l’ensemble des données qui portent sur les caractéristiques géographiques des objets (localisation, contours, liens). Les caractéristiques géographiques des objets sont décrites à l’aide d’un système de coordonnées. Celles-ci permettent de représenter l’objet géographique dans un espace euclidien à deux dimensions \((x,y)\). Le passage de l’espace réel (la Terre, qui est une sphère en trois dimensions) à l’espace plan se fait grâce à un système de projection.
1.2 Structure des données spatiales
Les données spatiales rassemblent classiquement deux types de données :
- des données géographiques (ou géométries) : objets géométriques tels que des points, des vecteurs, des polygones, ou des maillages (raster). Exemple: la forme de chaque commune, les coordonnées d’un bâtiment;
- des données attributaires (ou attributs) : des mesures et des caractéristiques associées aux objets géométriques. Exemple: la population de chaque commune, le nombre de fenêtres et le nombre d’étages d’un bâtiment.
Les données spatiales sont fréquemment traitées à l’aide d’un système d’information géographique (SIG), c’est-à-dire un système d’information capable de stocker, d’organiser et de présenter des données alphanumériques spatialement référencées par des coordonnées dans un système de référence (CRS). Python dispose de fonctionnalités lui permettant de réaliser les mêmes tâches qu’un SIG (traitement de données spatiales, représentations cartographiques).
1.3 Les données spatiales sont incontournables
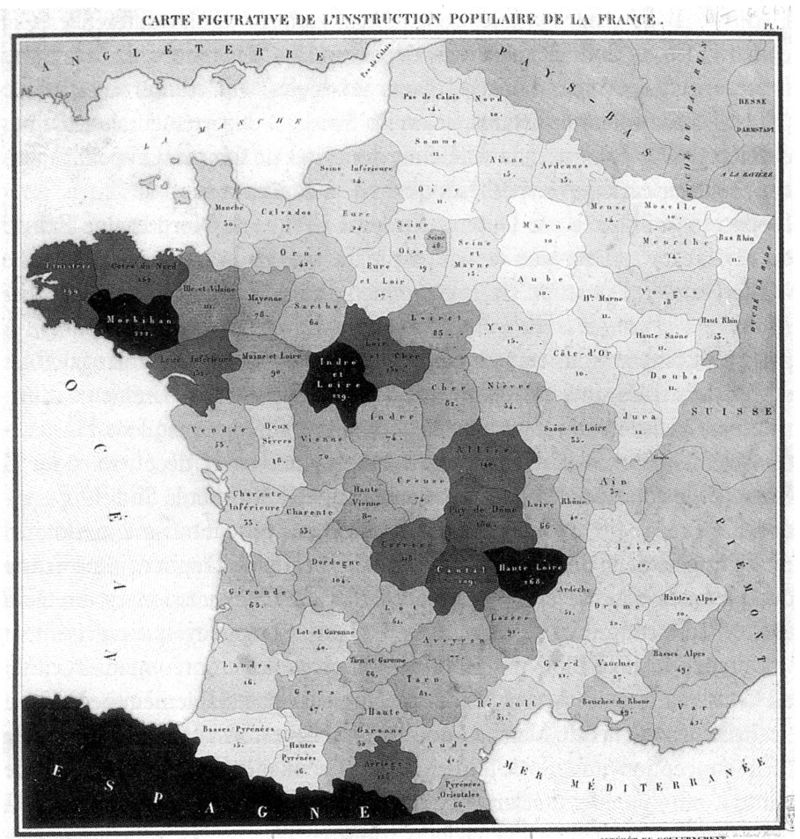
D’un usage initialement essentiellement militaire ou administratif, la production cartographique est, depuis au moins le XIXe siècle, très fréquente pour représenter de l’information socioéconomique. La représentation la plus connue dans ce domaine est la carte par aplat de couleur, dite carte choroplèthe1.
D’après Chen et al. (2008), la première représentation de ce type a été proposée par Charles Dupin en 1926 pour représenter les niveaux d’instruction sur le territoire français. L’émergence des cartes choroplèthes est en effet indissociable de l’organisation du pouvoir sous forme d’entités pensées politiques supposées unitaires: les cartes du monde représentent souvent des aplats de couleurs à partir des nations, les cartes nationales à partir d’échelons administratifs (régions, départements, communes, mais aussi Etats ou landers).
.
Si la production d’information géographique a pu être très liée à un usage militaire puis à la gestion administrative d’un territoire, la numérisation de l’économie ayant démultipliée les acteurs concernés par la collecte et la mise à disposition de données géographique, la manipulation et la représentation de données spatiales n’est plus l’apanage des géographes et géomaticiens. Les data scientists doivent être capables de rapidement explorer la structure d’un jeu de données géographique comme ils le feraient d’un jeu de données tabulaires classiques.
1.4 Où trouver la donnée spatiale française ?
Lors de notre périple de découverte de Pandas,
nous avons déjà rencontré quelques sources géolocalisées,
notamment produites par l’Insee. Cette institution publie
de nombreuses statistiques locales, par exemple les données
Filosofi que nous avons rencontrées au chapitre précédent. Au-delà
de l’Insee, l’ensemble des institutions du système
statistique public (Insee et services statistiques ministériels)
publie de nombreuses sources de données agrégées à différentes
mailles géographiques: à un niveau infracommunal (par exemple par carreaux de 200m),
au niveau communal ou à des niveaux supracommunaux (zonages administratifs ou zonages d’études).
Plus généralement, de nombreuses administrations françaises hors du système statistique public diffusent des données géographiques sur data.gouv. Nous avons par exemple précédemment exploité un jeu de données de l’Ademe dont la dimension géographique était la commune.
L’acteur central de l’écosystème public de la donnée géographique est l’IGN. Bien connu des amateurs de randonnées pour ses cartes “Top 25” qui peuvent être retrouvées sur le geoportail, l’IGN est également en charge de la cartographie des limites légales des entités administratives françaises (base AdminExpress), des forêts (BDForêt), des routes (BDRoute), des bâtiments (BDTopo), etc. Nous avons succinctement évoqué la librairie cartiflette lors du chapitre précédent, qui permet de récupérer les fonds de carte administratifs (base AdminExpress) de manière flexible avec Python ; nous irons plus loin dans ce chapitre.
La puissance publique n’est plus l’unique acteur qui produit et diffuse de la donnée spatiale. La collecte de coordonnées GPS étant devenue presque automatique, de nombreux acteurs collectent, exploitent et même revendent de la donnée spatiale sur leurs utilisateurs. Ces données peuvent être très précises et très riches sur certaines problématiques, par exemple sur les déplacements. Il est néanmoins nécessaire d’avoir à l’esprit lorsqu’on désire extrapoler des statistiques construites sur ces données que celles-ci concernent les utilisateurs du service en question, qui ne sont pas nécessairement représentatifs des comportements de la population dans son ensemble.
1.5 Objectifs de ce chapitre
Ce chapitre illustre à partir d’exemples pratiques certains principes centraux de l’analyse de données :
- Manipulations sur les attributs des jeux de données ;
- Manipulations géométriques ;
- Gestion des projections cartographiques ;
- Création rapide de cartes (ce sera approfondi dans un prochain chapitre).
1.6 Données utilisées dans ce chapitre
Dans ce tutoriel, nous allons utiliser les données suivantes :
- Localisations des stations velib ;
- fonds de carte
AdminExpressà travers un packagePythonnommécartiflettefacilitant la récupération de cette source.
1.7 Installations préalables
Ce tutoriel nécessite quelques installations de packages pour pouvoir être reproduit
Pour être en mesure d’exécuter ce tutoriel, les imports suivants seront utiles.
import geopandas as gpd
import contextily as ctx
import matplotlib.pyplot as plt
Warning
Le package cartiflette est expérimental
et n’est disponible que sur
Github, pas sur PyPi.
Il est amené à évoluer rapidement et cette page sera mise à jour
quand de nouvelles fonctionalités (notamment l’utilisation d’API)
seront disponibles pour encore simplifier la récupération de
contours géographiques.
Pour installer cartiflette, il est nécessaire d’utiliser les commandes suivantes
depuis un Jupyter Notebook (si vous utilisez la ligne de commande directement,
vous pouvez retirer les ! en début de ligne):
!pip install py7zr geopandas openpyxl tqdm s3fs
!pip install PyYAML xlrd
!pip install git+https://github.com/inseefrlab/cartiflette2 De Pandas à Geopandas
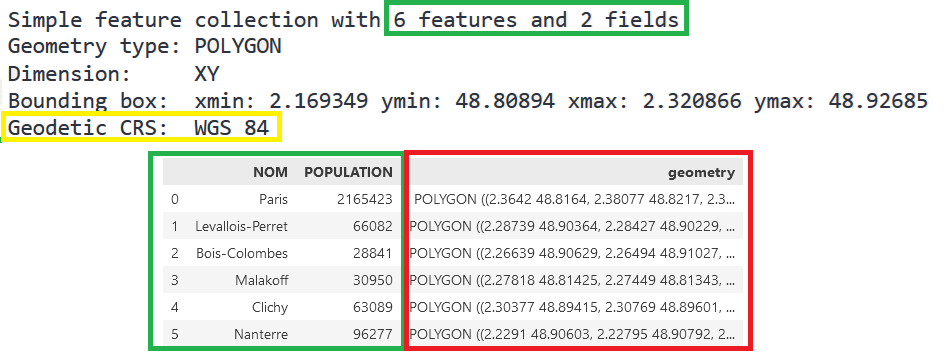
Le package Geopandas est une boîte à outils conçue pour faciliter la manipulation de données spatiales. La grande force de Geopandas est qu’il permet de manipuler des données spatiales comme s’il s’agissait de données traditionnelles, car il repose sur le standard ISO 19125 simple feature access défini conjointement par l’Open Geospatial Consortium (OGC) et l’International Organization for Standardization (ISO). Geopandas repose d’une part sur Pandas pour le traitement de la dimension tabulaire des données spatiales et d’autre part sur Shapely et GDAL pour les manipulations géométriques. Néanmoins, comme Pandas permettait de faire du Numpy sans le savoir, lorsqu’on travaille avec Geopandas on repose sur les deux couches basses que sont Shapely et GDAL sans avoir à s’embêter.
Par rapport à un DataFrame standard, un objet Geopandas comporte
une colonne supplémentaire: geometry. Elle stocke les coordonnées des
objets géographiques (ou ensemble de coordonnées s’agissant de contours). Un objet Geopandas hérite des propriétés d’un
DataFrame Pandas mais propose des méthodes adaptées au traitement des données spatiales. Par conséquent, grâce à GeoPandas, on a des attributs qui reposent sur le principe de données tidy évoquées dans le chapitre précédent alors que la géométrie afférante sera gérée de manière cohérente en parallèle des attributs.
Ainsi, grâce à Geopandas, on pourra effectuer des manipulations sur les attributs des données comme avec pandas mais on pourra également faire des manipulations sur la dimension spatiale des données. En particulier,
- Calculer des distances et des surfaces ;
- Agréger rapidement des zonages (regrouper les communes en département par exemple) ;
- Trouver dans quelle commune se trouve un bâtiment à partir de ses coordonnées géographiques ;
- Recalculer des coordonnées dans un autre système de projection ;
- Faire une carte, rapidement et simplement.
Tip
Les manipulations de données sur un objet Geopandas sont nettement plus lentes que sur
un DataFrame traditionnel (car Python doit gérer les informations géographiques pendant la manipulation des données).
Lorsque vous manipulez des données de grandes dimensions,
il peut être préférable d’effectuer les opérations sur les données avant de joindre une géométrie à celles-ci.
Par rapport à un logiciel spécialisé comme QGIS, Python permettra
d’automatiser le traitement et la représentation des données. D’ailleurs,
QGIS utilise lui-même Python…
2.1 Anatomie d’un objet GeoPandas
En résumé, un objet GeoPandas comporte les éléments suivants :
- Les attributs. Ce sont les valeurs associées à chaque niveau géographique.
Il s’agit de la dimension tabulaire usuelle, dont le traitement est similaire
à celui d’un objet
Pandasclassique. - Les géométries. Ce sont les valeurs numériques interprétées pour représenter la dimension géographique. Elles permettent de représenter dans un certain référentiel (le système de référence) la dimension géographique.
- Le système de référence. Il s’agit du système permettant de transformer les positions sur
le globe (3 dimensions avec une boule asymétrique) en un plan en deux dimensions.
Il en existe une multitude, identifiables à partir d’un code EPSG (4326, 2154…).
Leur manipulation est facilitée par
Geopandasqui s’appuie surShapely, de la même manière quePandass’appuie surNumpyouArrow.
3 Lire et enrichir des données spatiales
Dans le chapitre précédent, nous avons évoqué les formats de données
plats comme le CSV ou les nouveaux formats comme Parquet. Ceux-ci
sont adaptés à des données tabulaires.
Pour des données géographiques,
qui stockent de l’information selon plusieurs dimensions (les attributs
et la géométrie), il existe des formats spécialisés.
3.1 Le format shapefile (.shp) et le geopackage (.gpkg)
Le format historique de stockage de données spatiales est le shapefile. Il s’agit d’un format propriétaire, développé par ESRI, qui est néanmoins devenu une norme de facto. Dans ce format, la donnée est stockée dans plusieurs fichiers:
data.shp: contient les géométries des entités spatiales (points, lignes, polygones…).data.shx: un index pour accéder rapidement aux géométries stockées dans le fichier.shp.data.dbf: une table attributaire au format dBase qui contient les informations descriptives des entités spatiales.data.prj: contient les informations de projection et de système de coordonnées (nous reviendrons sur ce concept ultérieurement).
Ce format présente plusieurs inconvénients. Tout d’abord il est assez volumineux ; certains formats modernes seront plus optimisés pour réduire la volumétrie sur disque et le temps de chargement des données. Surtout, le problème principal du shapefile est que pour lire les données de manière intègre, il est nécessaire de partager de manière systématique ces quatre fichiers, sous peine d’introduire un risque de corruption ou d’incomplétude de la donnée. En faisant gpd.read_file("data.shp"), GeoPandas
fait lui-même le lien entre les observations et leur représentation spatiale qui sont présents dans plusieurs fichiers.
Le format GeoPackage est un héritier spirituel du shapefile visant à résoudre ces deux limites. Il s’agit d’un format libre recommandé par l’open geospatial consortium (OGC). Les géomaticiens apprécient ce format, il s’agit d’ailleurs du format par défaut de QGIS, le logiciel spécialisé pour les SIG. Néanmoins, même si GeoPandas fonctionne bien avec ce format, celui-ci est moins connu par les data scientists que le shapefile ou que le geojson que nous allons décrire par la suite.
3.2 Le GeoJSON et le TopoJSON
Le développement d’un format concurrent l’hégémonie du shapefile est intrinsèquement lié à l’émergence des technologies web dans le secteur de la cartographie. Ces technologies web s’appuient sur Javascript et reposent sur les standards du format JSON.
Le format GeoJSON stocke dans un seul fichier à la fois les attributs et les géométries. Il est donc assez pratique à l’usage et s’est imposé comme le format préféré des développeurs web. Le fait de stocker l’ensemble de l’information dans un seul fichier peut cependant le rendre assez volumineux si les géométries sont très précises, mais le volume reste moindre que celui du shapefile. GeoPandas est très bien fait pour lire des fichiers au format GeoJSON et les plateformes de partage de données, comme data.gouv privilégient ce format à celui du shapefile.
Pour alléger le fichier, le format TopoJSON a récémment émergé. Celui-ci est construit selon les mêmes principes que le GeoJSON mais réduit le volume de données géométriques stockées en ne conservant pas tous les points en appliquant une simplification pour ne conserver que les arcs et les directions entre ceux-ci. Ce format étant récent, il n’est pas encore bien intégré à l’écosystème Python.
3.3 Les autres formats de données
L’écosystème des formats de données géographiques est bien plus éclaté que celui des données structurées. Chaque format présente des avantages qui le rendent intéressant pour un type de données mais des limites qui l’empêchent de devenir un standard pour d’autres types de données.
Par exemple, les données GPS extraites de diverses applications (par exemple Strava) sont stockées au format GPX. Ce dernier est particulièrement adapté pour des traces géolocalisées avec une altitude. Mais ce n’est pas le format le plus approprié pour stocker des lignes directionnelles, un prérequis indispensable pour les applications d’itinéraires.
Les formats shapefile et geojson sont suffisamment malléables pour s’adapter aux différents types de données géographiques même s’il ne s’agit
pas du format optimal pour tel ou tel type de données. Dans cette classe généraliste de formats, le Geoparquet pourrait être le prochain format à la mode. Comme son nom l’indique, il s’agit d’une extension du format Parquet à des données géographiques. Ce format n’est pas encore mûr mais reste à suivre, la masse d’utilisateurs de l’écosystème Parquet pouvant amener à un changement rapide si une implémentation stable de Geoparquet émerge.
Cette page compare plus en détail les principes formats de données géographiques.
L’aide de Geopandas propose des bouts de code en fonction des différentes situations dans lesquelles on se trouve.
3.4 Exercice de découverte
L’objectif de cet exercice est d’illustrer la similarité des objets
GeoPandas avec les objets Pandas que nous avons découverts précédemment.
Nous allons importer directement les données AdminExpress (limites officielles des communes produites par l’IGN) avec cartiflette:
Exercice 1: découverte des objets géographiques
En premier lieu, on récupère des données géographiques grâce
au package cartiflette et à sa fonction carti_download.
Utiliser le code sous cet exercice (celui utilisant
carti_download) pour télécharger les contours communaux des départements de la petite couronne (75, 92, 93 et 94) de manière simplifiée grâce au packagecartifletteRegarder les premières lignes des données. Identifier la différence avec un dataframe standard.
Afficher le système de projection (attribut
crs) decommunes_borders. Ce dernier contrôle la transformation de l’espace tridimensionnel terrestre en une surface plane. Utiliserto_crspour transformer les données en Lambert 93, le système officiel (code EPSG 2154).Afficher les communes des Hauts de Seine (département 92) et utiliser la méthode
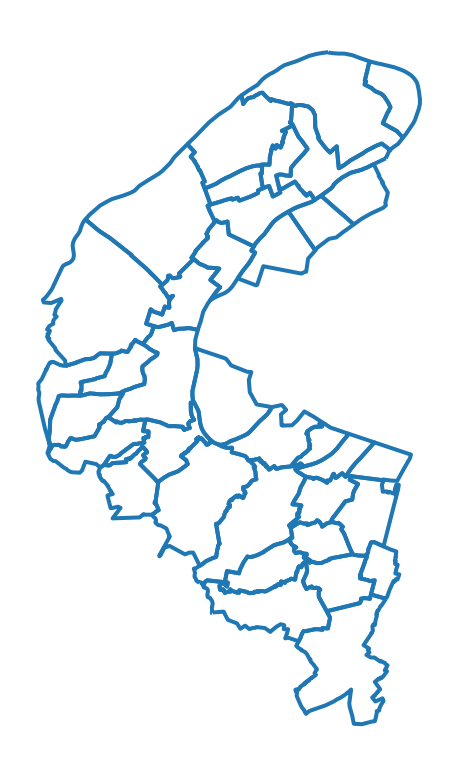
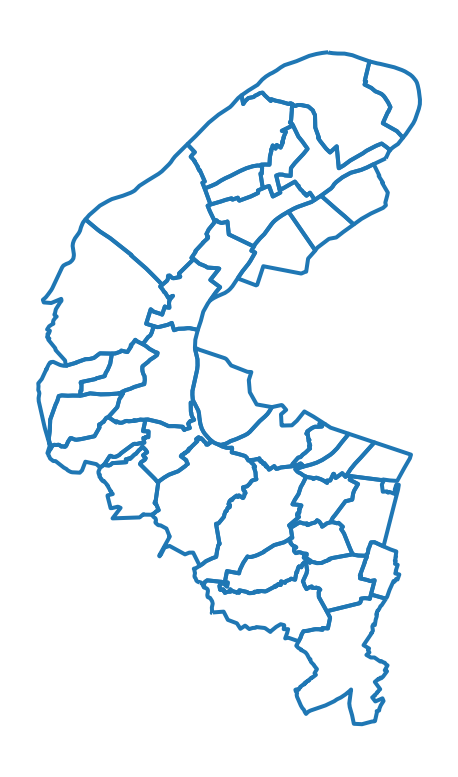
plotNe conserver que Paris et réprésenter les frontières sur une carte : quel est le problème pour une analyse de Paris intramuros?
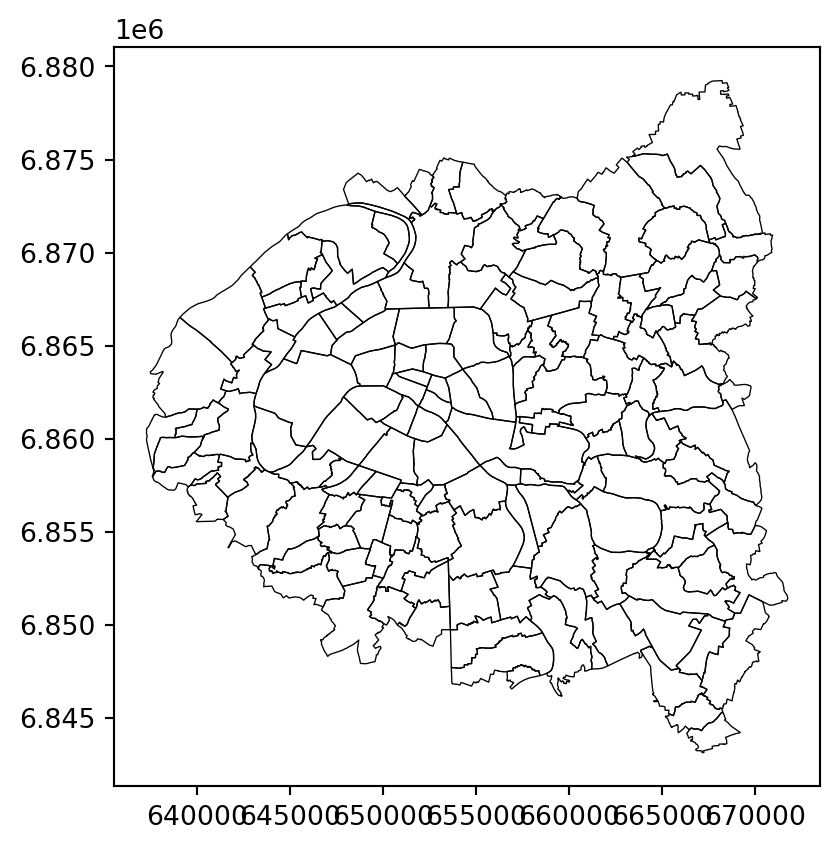
On remarque rapidement le problème. On ne dispose ainsi pas des limites des arrondissements parisiens, ce qui appauvrit grandement la carte de Paris.
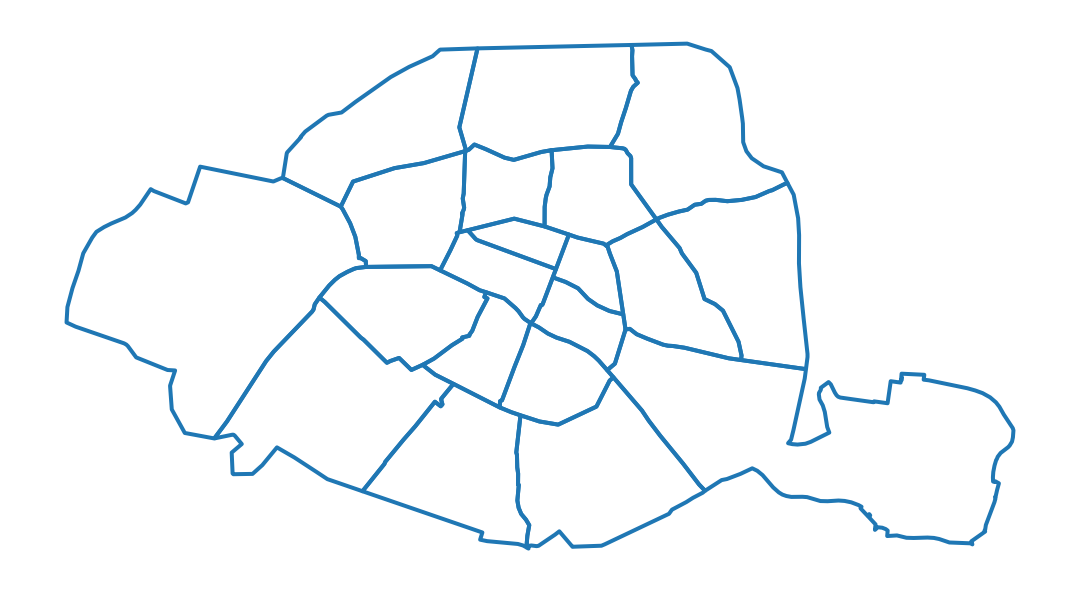
- Cette fois, utiliser l’argument
borders="COMMUNE_ARRONDISSEMENT"pour obtenir un fonds de carte consolidé des communes avec les arrondissements dans les grandes villes. Convertir en Lambert 93.
# 1. Chargement des données de Cartiflette
from cartiflette import carti_download
communes_borders = carti_download(
crs=4326,
values=["75", "92", "93", "94"],
borders="COMMUNE",
vectorfile_format="geojson",
filter_by="DEPARTEMENT",
source="EXPRESS-COG-CARTO-TERRITOIRE",
year=2022,
)La visualisation proposée à la question permet de voir que notre DataFrame comporte la colonne geometry qui contient les informations nécessaires pour connaître les contours communaux.
<Geographic 2D CRS: EPSG:4326>
Name: WGS 84
Axis Info [ellipsoidal]:
- Lat[north]: Geodetic latitude (degree)
- Lon[east]: Geodetic longitude (degree)
Area of Use:
- name: World.
- bounds: (-180.0, -90.0, 180.0, 90.0)
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: GreenwichLes données sont en WGS84, on les reprojette en Lambert 93
A la question 5, on remarque facilement le problème pour Paris: il manque les limites des arrondissements. Cela appauvrit grandement la carte de Paris.
A l’issue de la question 6, on obtient la carte attendue pour Paris intramuros:
4 Le système de projection cartographique
4.1 Principe
Les données spatiales sont plus riches que les données traditionnelles car elles incluent, habituellement, des éléments supplémentaires pour placer dans un espace cartésien les objets. Cette dimension supplémentaire peut être simple (un point comporte deux informations supplémentaire: \(x\) et \(y\)) ou assez complexe (polygones, lignes avec direction, etc.).
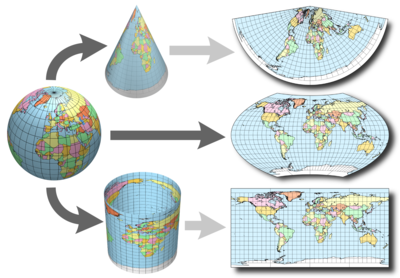
L’analyse cartographique emprunte dès lors à la géométrie des concepts pour représenter des objets dans l’espace. Les projections sont au coeur de la gestion des données spatiales. Ces dernières consistent à transformer une position dans l’espace terrestre à une position sur un plan. Il s’agit donc d’une opération de projection d’un espace tri-dimensionnel dans un espace à deux dimensions. Ce post propose de riches éléments sur le sujet, notamment l’image suivante qui montre bien le principe d’une projection :
Cette opération n’est pas neutre. L’une des conséquences du théorème remarquable de Gauss est que la surface de la Terre ne peut être cartographiée sans distortion. Une projection ne peut simultanément conserver intactes les distances et les angles (i.e. les positions). Il n’existe ainsi pas de projection universellement meilleure, ce qui ouvre la porte à la coexistence de nombreuses projections différentes, pensées pour des tâches différentes. Un mauvais système de représentation fausse l’appréciation visuelle mais peut aussi entraîner des erreurs dans les calculs sur la dimension spatiale.
Les systèmes de projection font l’objet de standards internationaux et sont souvent désignés par des codes dits codes EPSG. Ce site est un bon aide-mémoire. Les plus fréquents, pour les utilisateurs français, sont les suivants (plus d’infos ici) :
2154: système de projection Lambert 93. Il s’agit du système de projection officiel. La plupart des données diffusées par l’administration pour la métropole sont disponibles dans ce système de projection.27572: Lambert II étendu. Il s’agit de l’ancien système de projection officiel. Les données spatiales anciennes peuvent être dans ce format.4326: WGS 84 ou système de pseudo-Mercator Ce n’est en réalité pas un système de projection mais un système de coordonnées (longitude / latitude) qui permet simplement un repérage angulaire sur l’ellipsoïde. Il est utilisé pour les données GPS. Il s’agit du système le plus usuel, notamment quand on travaille avec des fonds de carte web.
4.2 Le système Mercator
Comme évoqué plus haut, l’une des projections les plus connues est la projection Web Mercator (code EPSG 3857), qui projète sur les cartes planes les données sphériques de longitude, latitude issues du système WGS84 (EPSG 4326), qui est le système géodésique utilisé par le GNSS américain GPS, utilisé par l’immense majorité des systèmes de navigation mondiaux, et a fortiori Google Maps. Il s’agit d’une projection conservant intacte les angles, ce qui implique qu’elle altère les distances. Celle-ci a en effet été pensée, à l’origine, pour représenter l’hémisphère Nord. Plus on s’éloigne de celui-ci, plus les distances sont distordues. Cela amène à des distorsions bien connues (le Groenland hypertrophié, l’Afrique de taille réduite, l’Antarctique démesuré…). En revanche, la projection Mercator conserve intacte les positions. C’est cette propriété qui explique son utilisation dans les systèmes GPS et ainsi dans les fonds de carte de navigation du type Google Maps. Il s’agit d’une projection pensée d’abord pour la navigation, non pour la représentation d’informations socioéconomiques sur la terre. Cette projection est indissociable des grandes explorations de la Renaissance, comme le rappelle ce fil sur Twitter de Jules Grandin.
Reddit
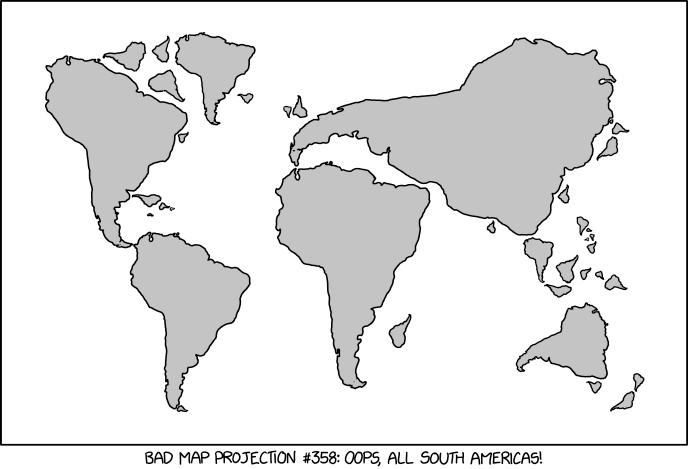
Observez les variations significatives de proportions pour certains pays selon les projections choisies:
Pour aller plus loin, la carte interactive
suivante, construite par Nicolas Lambert, issue de
ce notebook Observable, illustre l’effet
déformant de la projection Mercator, et de quelques-unes autres,
sur notre perception de la taille des pays.
Voir la carte interactive
Il existe en fait de nombreuses représentations possibles du monde, plus ou moins alambiquées. Les projections sont très nombreuses et certaines peuvent avoir une forme suprenante. Par exemple, la projection de Spillhaus propose de centrer la vue sur les océans et non une terre. C’est pour cette raison qu’on parle parfois de monde tel que vu par les poissons à son propos.
Astuce pour la France
Pour la France, dans le système WGS84 (4326) :
- Longitude (\(x\)) tourne autour de 0° (de -5.2 à +9.6 pour être plus précis)
- La latitude (\(y\)) autour de 45 (entre +41.3 à +51.1)
Dans le système Lambert 93 (2154) :
- Coordonnées \(x\): entre 100 000 et 1 300 000
- La latitude (\(y\)): entre 6 000 000 et 7 200 000
4.3 Gestion avec GeoPandas
Concernant la gestion des projections avec GeoPandas,
la documentation officielle est très bien
faite. Elle fournit notamment l’avertissement suivant qu’il est
bon d’avoir en tête :
Be aware that most of the time you don’t have to set a projection. Data loaded from a reputable source (using the geopandas.read_file() command) should always include projection information. You can see an objects current CRS through the GeoSeries.crs attribute.
From time to time, however, you may get data that does not include a projection. In this situation, you have to set the CRS so geopandas knows how to interpret the coordinates.
Les deux principales méthodes pour définir le système de projection utilisé sont :
df.set_crs: cette commande sert à préciser quel est le système de projection utilisé, c’est-à-dire comment les coordonnées (x,y) sont reliées à la surface terrestre. Cette commande ne doit pas être utilisée pour transformer le système de coordonnées, seulement pour le définir.df.to_crs: cette commande sert à projeter les points d’une géométrie dans une autre, c’est-à-dire à recalculer les coordonnées selon un autre système de projection.
Dans le cas particulier de production de carte avec un fond OpenStreetMaps ou une carte dynamique leaflet, il est nécessaire de dé-projeter les données (par exemple à partir du Lambert-93) pour atterrir dans le système non-projeté WGS 84 (code EPSG 4326). Ce site dédié aux projections géographiques peut être utile pour retrouver le système de projection d’un fichier où il n’est pas indiqué.
Le prochain exercice permettra, avec quelques cas pathologiques, de se convaincre de l’importance de déléguer le plus possible la gestion du système de projection à GeoPandas. La question n’est pas que sur la pertinence de la représentation des objets géographiques sur la carte. En effet, l’ensemble des opérations géométriques (calculs d’aires, de distance, etc.) peut être affecté par les choix faits sur le système de projection.
4.4 Exercice pour comprendre l’importance du système de projection
Voici un code utilisant encore
cartiflette
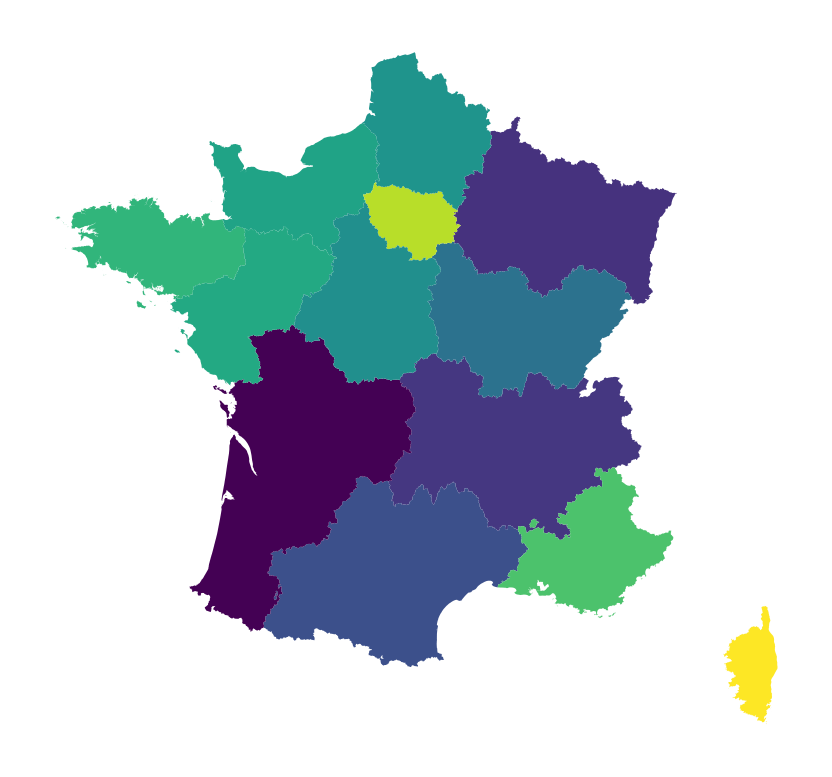
pour récupérer les frontières françaises (découpées par région):
from cartiflette import carti_download
france = carti_download(
values=["France"],
crs=4326,
borders="REGION",
vectorfile_format="geojson",
simplification=50,
filter_by="FRANCE_ENTIERE",
source="EXPRESS-COG-CARTO-TERRITOIRE",
year=2022,
)
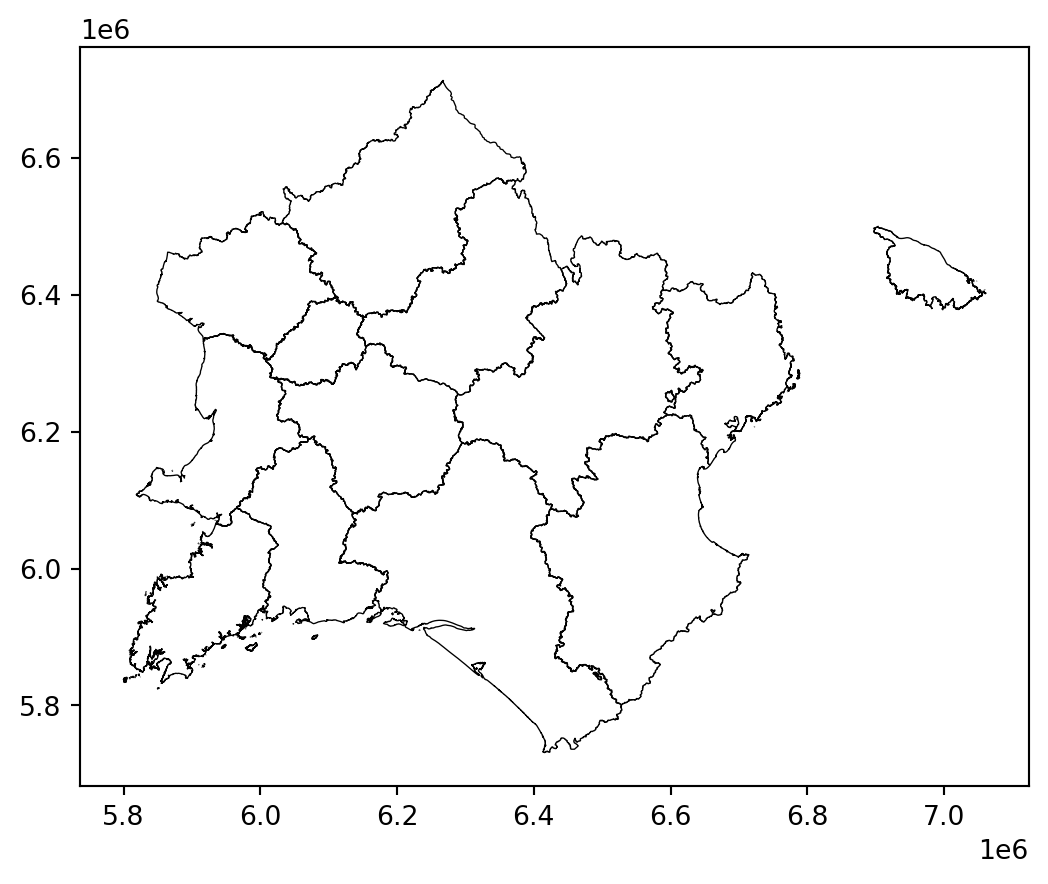
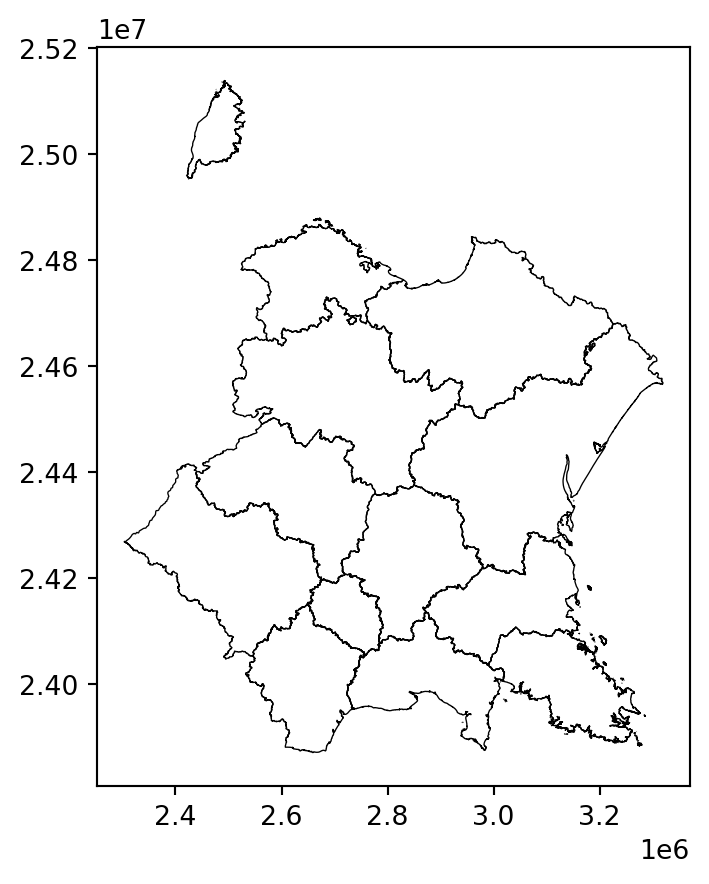
france = france.loc[france["INSEE_REG"] > 10]
Exercice 2 : Les projections, représentations et approximations
- S’amuser à représenter les limites de la France avec plusieurs projections:
- Mercator WGS84 (EPSG: 4326)
- Projection healpix (
+proj=healpix +lon_0=0 +a=1) - Projection prévue pour Tahiti (EPSG: 3304)
- Projection Albers prévue pour Etats-Unis (EPSG: 5070)
- Calculer la superficie en \(km^2\) des régions françaises dans les deux systèmes de projection suivants : World Mercator WGS84 (EPSG: 3395) et Lambert 93 (EPSG: 2154). Calculer la différence en \(km^2\) pour chaque région.
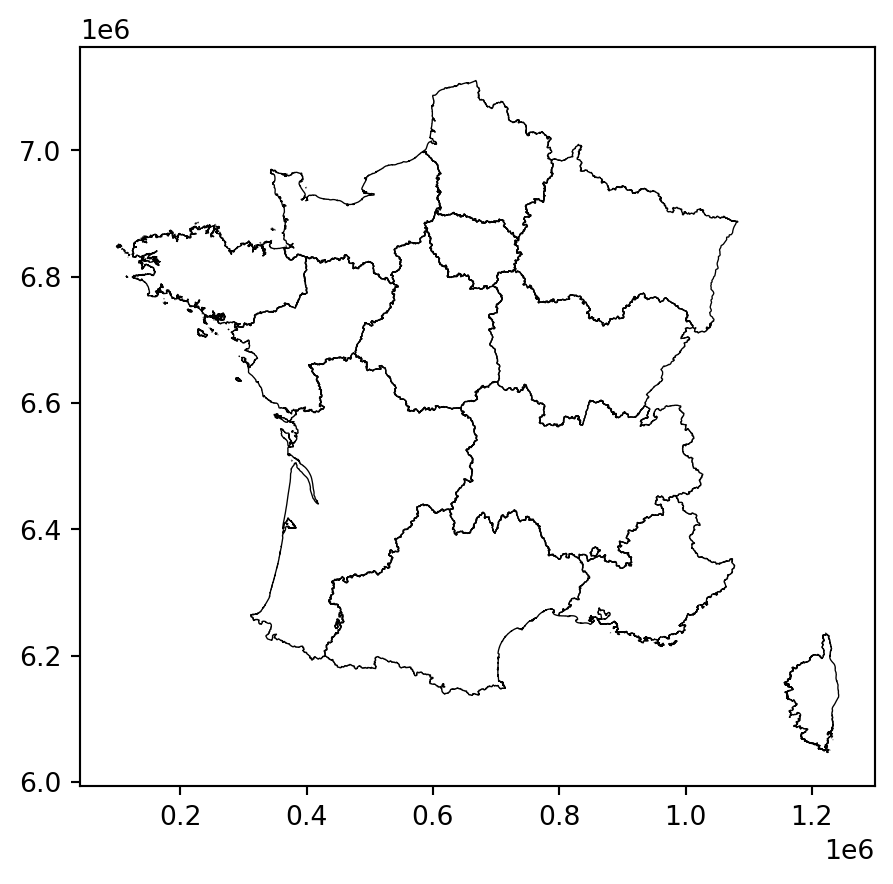
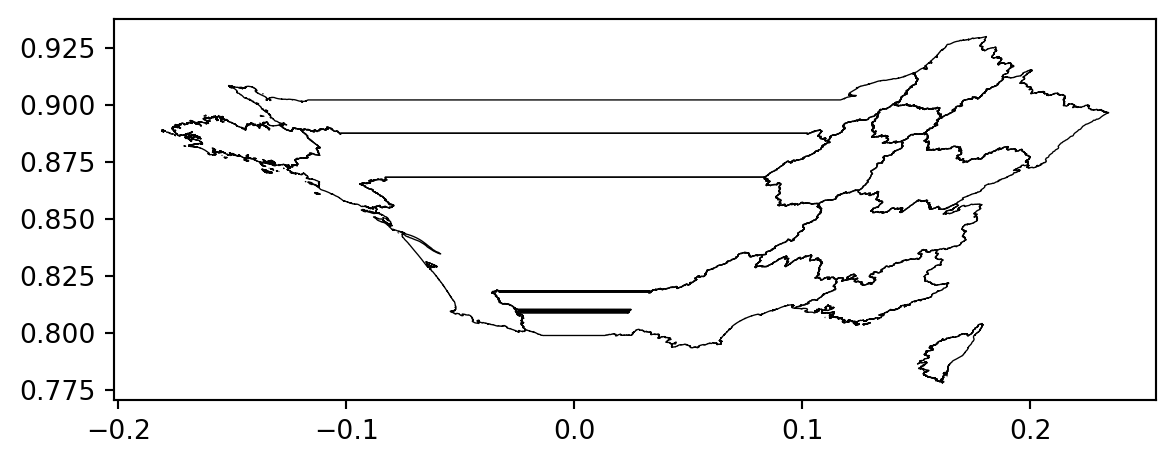
Avec la question 1 illustrant quelques cas pathologiques, on comprend que les projections ont un effet déformant qui se voit bien lorsqu’on les représente côte à côte sous forme de cartes :
Cependant le problème n’est pas que visuel, il est également numérique. Les calculs géométriques amènent à des différences assez notables selon le système de référence utilisé.
On peut représenter ces approximations sur une carte2 pour se faire une idée des régions où l’erreur de mesure est la plus importante (objet de la question 2).
Ce type d’erreur de mesure est normal à l’échelle du territoire français. Les projections héritères du Mercator déforment les distances, surtout lorsqu’on se rapproche de l’équateur ou des pôles.
Il faut donc systématiquement repasser les données dans le système de projection Lambert 93 (le système officiel pour la métropole) avant d’effectuer des calculs géométriques.
5 Importer et explorer les jeux de données spatiaux
Souvent, le découpage communal ne sert qu’en fond de cartes, pour donner des repères. En général, il sert donc à contextualiser un autre jeu de données.
Pour illustrer cette approche, on va partir des données de localisation et de capacités des stations velib, disponibles sur le site d’open data de la ville de Paris et requêtables directement par l’url https://opendata.paris.fr/explore/dataset/velib-emplacement-des-stations/download/?format=geojson&timezone=Europe/Berlin&lang=fr. Ce jeu de données nous permettra d’illustrer quelques enjeux classiques de l’analyse de données spatiales
velib_data = "https://opendata.paris.fr/explore/dataset/velib-emplacement-des-stations/download/?format=geojson&timezone=Europe/Berlin&lang=fr"
stations = gpd.read_file(velib_data)
stations.head(2)Skipping field coordonnees_geo: unsupported OGR type: 3| capacity | name | stationcode | geometry | |
|---|---|---|---|---|
| 0 | 20 | Charonne - Robert et Sonia Delaunay | 11104 | POINT (2.39257 48.85591) |
| 1 | 52 | Morillons - Dantzig | 15047 | POINT (2.29938 48.8331) |
5.1 Localiser les données sur une carte
La première étape, avant l’exploration approfondie des données, consiste à afficher celles-ci sur une carte contextuelle, afin de s’assurer de l’emprise géographique des données. Dans notre cas, cela nous donnera une intuition sur la localisation des stations et notamment la densité hétérogène de celles-ci dans l’espace urbain parisien.
5.2 Exercice d’application
Dans le prochain exercice, nous proposons de créer rapidement une carte comprenant trois couches :
- Les localisations de stations sous forme de points ;
- Les bordures des communes et arrondissements pour contextualiser ;
- Les bordures des départements en traits plus larges pour contextualiser également.
Nous irons plus loin dans le travail cartographique dans le prochain chapitre. Mais être en mesure de positionner rapidement ses données sur une carte est toujours utile dans un travail exploratoire.
En amont de l’exercice,
utiliser la fonction suivante du package cartiflette pour récupérer
le fonds de carte des départements de la petite couronne:
idf = carti_download(
values=["11"],
crs=4326,
borders="DEPARTEMENT",
vectorfile_format="geojson",
filter_by="REGION",
source="EXPRESS-COG-CARTO-TERRITOIRE",
year=2022,
)
petite_couronne_departements = idf.loc[
idf["INSEE_DEP"].isin(["75", "92", "93", "94"])
].to_crs(2154)
Exercice 3: importer et explorer les données velib
On commence par récupérer les données nécessaires à la production de cette carte.
- Vérifier la projection géographique de
station(attributcrs). Si celle-ci est différente des données communales, reprojeter ces dernières dans le même système de projection que les stations de vélib - Ne conserver que les 50 principales stations (variable
capacity)
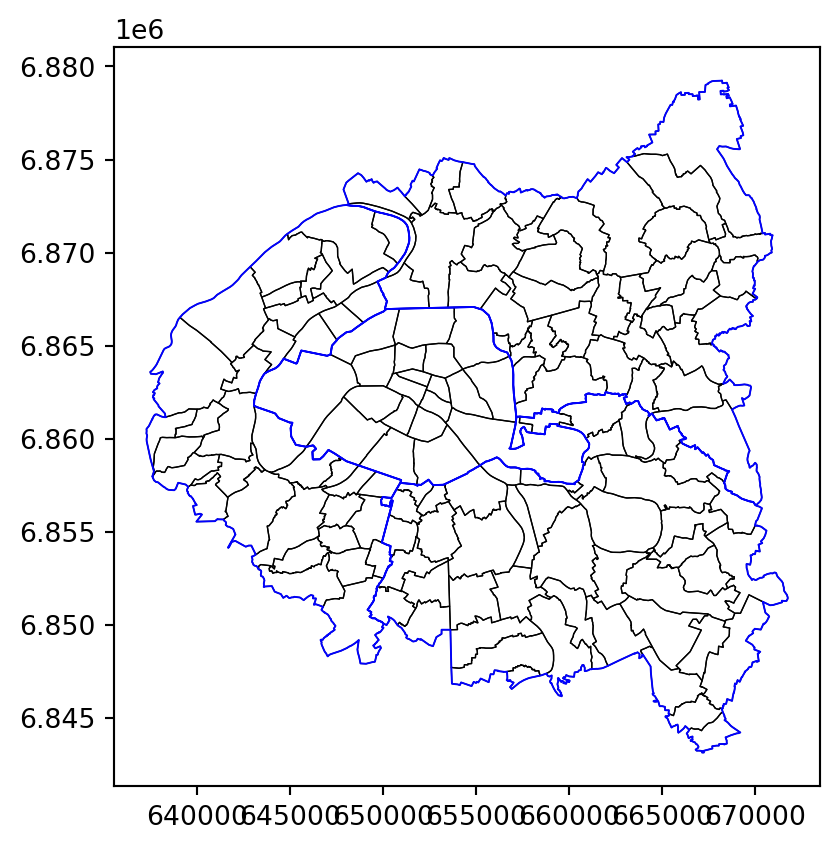
On peut maintenant construire la carte de manière séquentielle avec la méthode plot en s’aidant de cette documentation
En premier lieu, grâce à
boundary.plot, représenter la couche de base des limites des communes et arrondissements:- Utiliser les options
edgecolor = "black"etlinewidth = 0.5 - Nommer cet objet
base
- Utiliser les options
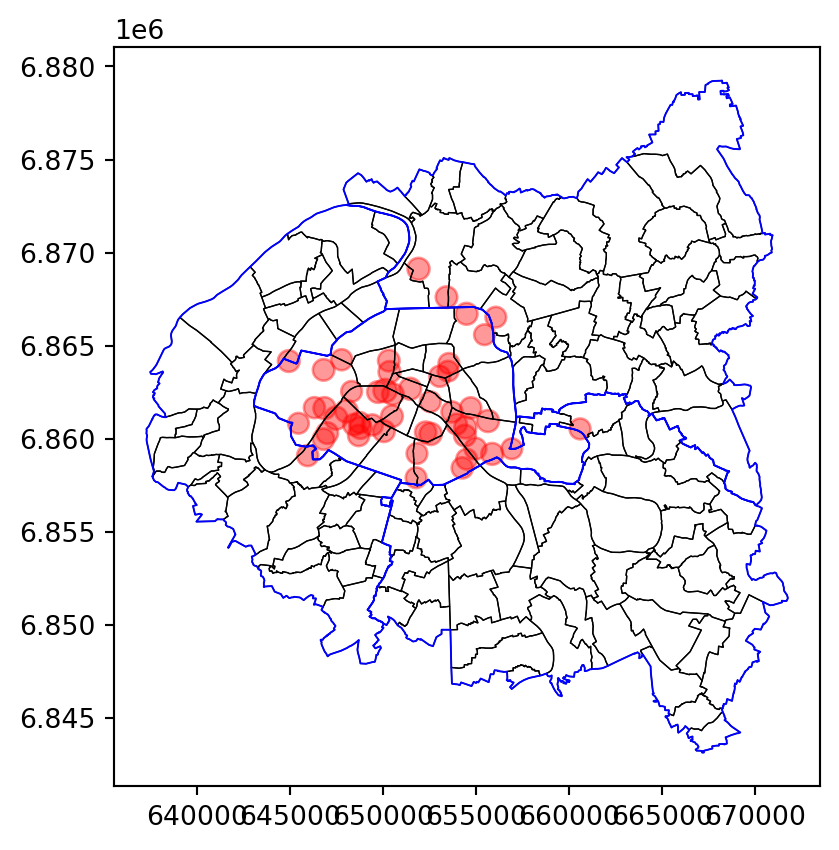
Ajouter la couche des départements avec les options
edgecolor = "blue"etlinewidth = 0.7Ajouter les positions des stations et ajuster la taille en fonction de la variable
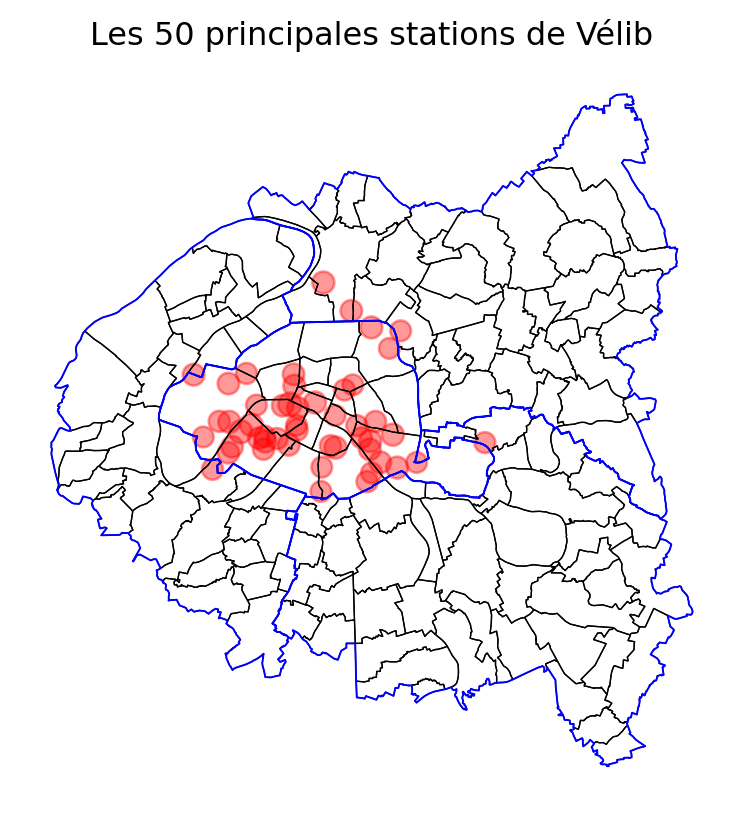
capacity. L’esthétique des points obtenus peut être contrôlé grâce aux optionscolor = "red"etalpha = 0.4.Retirer les axes et ajouter un titre avec les options ci-dessous:
base.set_axis_off()
base.set_title("Les 50 principales stations de Vélib")- En suivant le modèle suivant, grâce au package
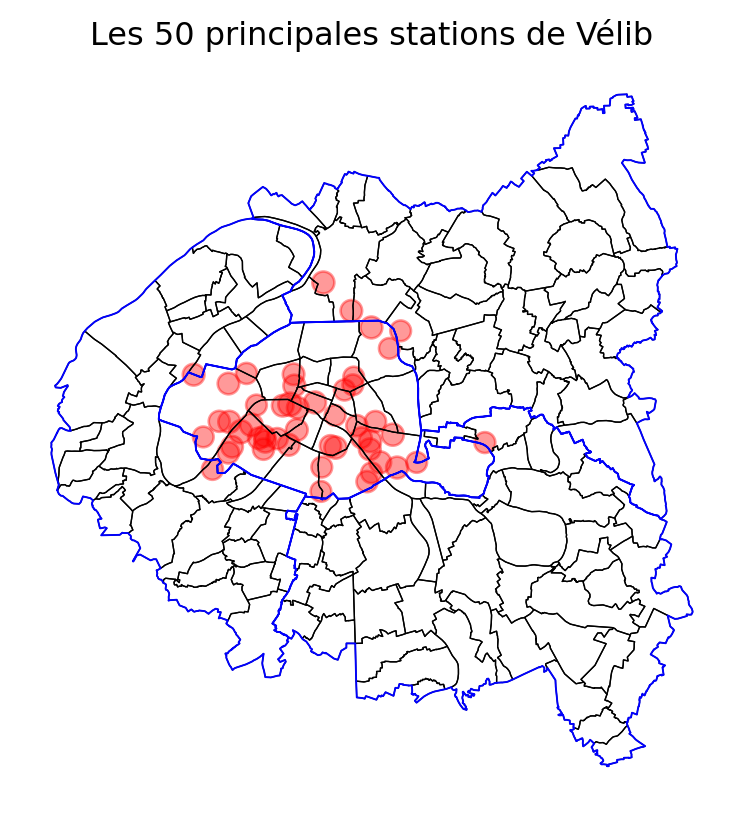
contextily, ajouter un fond de carte contextuel openstreetmap
import contextily as ctx
ax = ...
ctx.add_basemap(ax, source=ctx.providers.OpenStreetMap.Mapnik)⚠️ contextily attend des données dans le système de représentation Pseudo Mercator (EPSG: 3857), il sera donc nécessaire de reprojeter vos données avant de réaliser la carte.
La couche de base obtenue à l’issue de la question 3
Puis en y ajoutant les limites départementales (question 4).
Puis les stations (question 5).
Ensuite, si on retire les axes (question 6), on obtient:
La carte est déjà parlante en soi. Néanmoins, pour des personnes moins familières de la géographie parisienne, elle pourrait être encore plus limpide avec l’ajout d’un fond de carte contextuel openstreetmap. In fine, cela donne la carte suivante:
<Axes: title={'center': 'Les 50 principales stations de Vélib'}><Figure size 672x480 with 0 Axes>5.3 Opérations sur les géométries
Outre la représentation graphique simplifiée,
l’intérêt principal d’utiliser
GeoPandas est l’existence de méthodes efficaces pour
manipuler la dimension spatiale. Un certain nombre proviennent du
package
Shapely.
Nous avons déjà vu la méthode to_crs pour reprojeter les données de manière vectorisée sans avoir à s’inquiéter.
Nous avons également évoqué la méthode area
pour calculer des surfaces. Il en existe de nombreuses et l’objectif de ce chapitre n’est pas d’être exhaustif sur le sujet mais plutôt de servir d’introduction générale pour amener à approfondir ultérieurement.
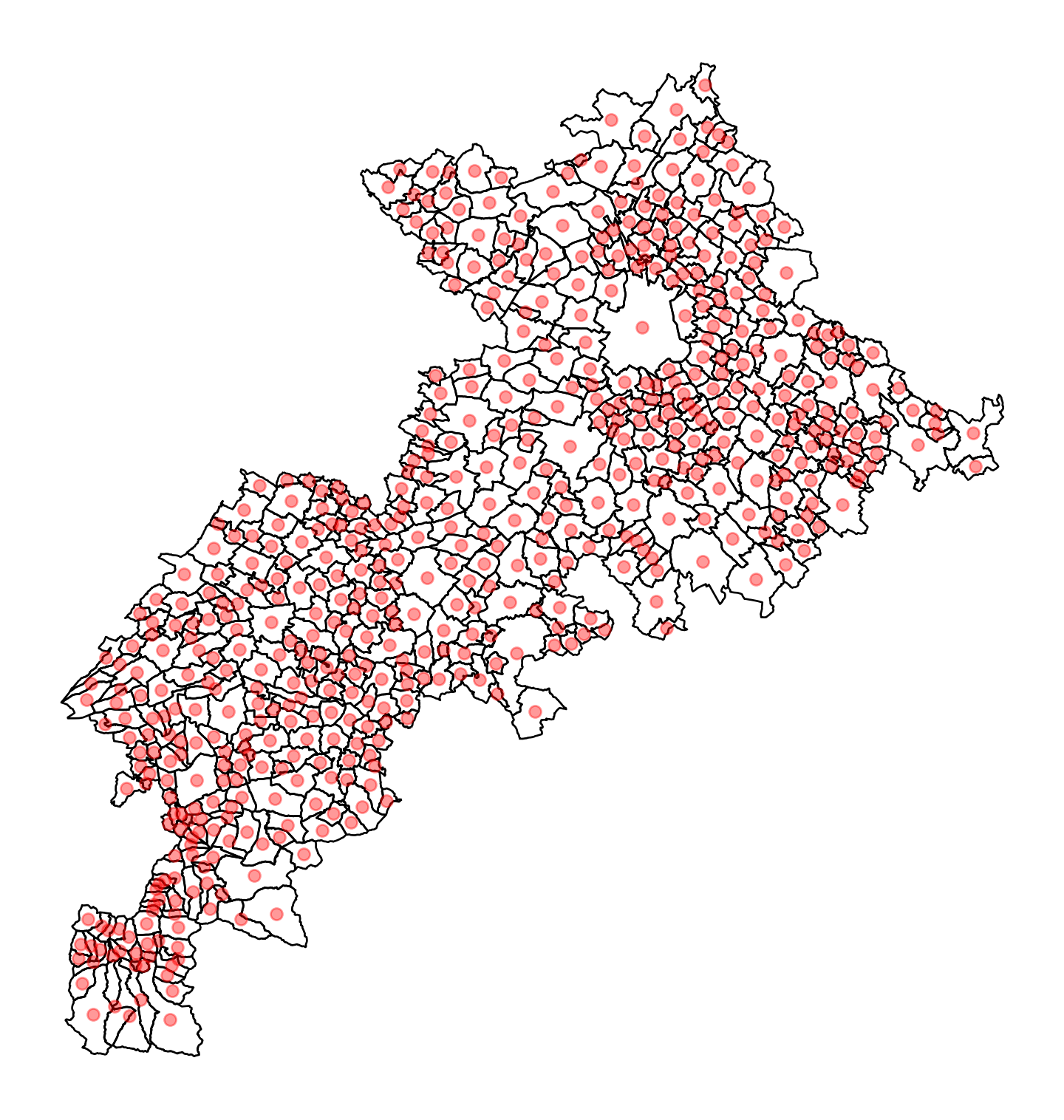
Parmi les méthodes les plus utiles, on peut citer centroid qui, comme son nom l’indique,
recherche le centroïde de chaque polygone et transforme ainsi des données
surfaciques en données ponctuelles. Par exemple, pour
représenter approximativement les centres des villages de la
Haute-Garonne (31), après avoir téléchargé le fonds de carte adapté, on
fera
from cartiflette import carti_download
communes_31 = carti_download(
values=["31"],
crs=4326,
borders="COMMUNE",
vectorfile_format="geojson",
filter_by="DEPARTEMENT",
source="EXPRESS-COG-CARTO-TERRITOIRE",
year=2022,
)
# on reprojete en 3857 pour le fond de carte
communes_31 = communes_31.to_crs(3857)
# on calcule le centroide
dep_31 = communes_31.copy()
communes_31["geometry"] = communes_31["geometry"].centroid
ax = communes_31.plot(figsize=(10, 10), color="red", alpha=0.4, zorder=2)
dep_31.to_crs(3857).plot(
ax=ax, zorder=1, edgecolor="black", facecolor="none", color=None
)
# ctx.add_basemap(ax, source = ctx.providers.Stamen.Toner)
ax.set_axis_off()
ax
Par conséquent, avec Geopandas, l’ensemble de la grammaire Pandas peut être mobilisée pour traiter la dimension attributaire des données alors que la dimension géographique pourra être manipulée avec des méthodes adaptées.
6 Enrichissements grâce à la dimension spatiale: les jointures spatiales
6.1 Principe
La carte précédente illustre déjà la puissance de la représentation cartographique. En quelques lignes de code, avec très peu d’opérations sur nos données, on comprend déjà mieux le phénomène qu’on désire observer. En l’occurrence, on détecte très clairement une structure centre-périphérie dans nos données, ce qui n’est pas surprenant mais qu’il est rassurant de retrouver au premier abord.
On remarque également que les stations les plus utilisées, à l’extérieur de l’hypercentre parisien, sont généralement situées sur les grands axes ou à proximité des parcs. Là encore, rien de surprenant mais il est rassurant de retrouver ceci dans nos données.
On peut maintenant explorer de manière plus approfondie la structure de notre jeu de données. Cependant si on observe celui-ci, on remarque qu’on a peu d’informations dans le jeu de données brutes
stations.head(2)| capacity | name | stationcode | geometry | |
|---|---|---|---|---|
| 0 | 20 | Charonne - Robert et Sonia Delaunay | 11104 | POINT (655430.484 6861934.722) |
| 1 | 52 | Morillons - Dantzig | 15047 | POINT (648570.38 6859455.565) |
Dans le chapitre précédent, nous avons présenté la manière dont l’association de jeux de données par une dimension commune permet d’accroître la valeur de celles-ci. En l’occurrence, il s’agissait d’appariements de données sur la base d’informations communes dans les deux jeux de données.
Nous avons maintenant une information supplémentaire implicite dans nos deux de données: la dimension géographique. On parle de jointure spatiale pour désigner l’association de jeux de données sur la dimension géographique. Il existe de nombreux types différents de jointures spatiales: trouver des points dans un polygone, trouver l’intersection entre plusieurs aires, relier un point à son plus proche voisin dans une autre source, etc.
6.2 Exemple: localiser les stations dans leur arrondissement
Dans cet exercice, on va supposer que :
- les localisations des stations
velibsont stockées dans un dataframe nomméstations - les données administratives
sont dans un dataframe nommé
petite_couronne.
Exercice 4: Associer les stations aux communes et arrondissements auxquels elles appartiennent
- Faire une jointure spatiale pour enrichir les données de stations en y ajoutant des informations de
petite_couronne. Appeler cet objetstations_info. - Compter le nombre de stations et la taille médiane des stations par arrondissements
- Créer les objets
stations_19eetarrondissement_19epour stocker, respectivement, les stations appartenant au 19e et les limites de l’arrondissement. - Compter le nombre de stations velib et le nombre de places velib par arrondissement ou commune. Représenter sur une carte chacune des informations
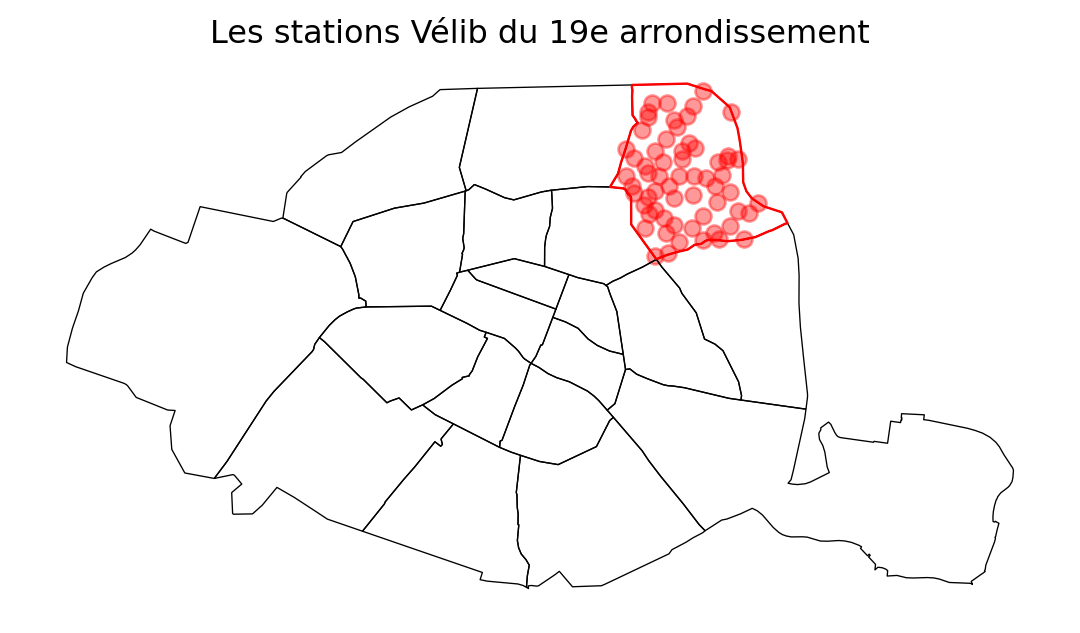
- Représenter la carte des stations du 19e arrondissement avec le code suivant :
base = petite_couronne.loc[petite_couronne["INSEE_DEP"] == "75"].boundary.plot(
edgecolor="k", linewidth=0.5
)
arrondissement_19e.boundary.plot(ax=base, edgecolor="red", linewidth=0.9)
stations_19.plot(ax=base, color="red", alpha=0.4)
base.set_axis_off()
base.set_title("Les stations Vélib du 19e arrondissement")
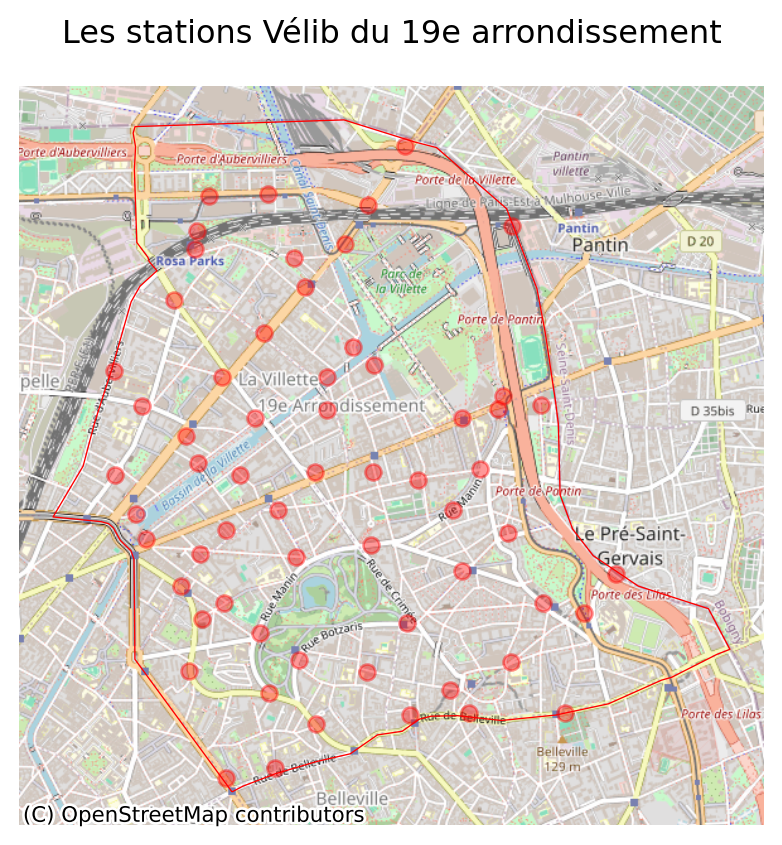
baseEn reprenant les exemples précédents, ne représenter que le 19e et ajouter un fond de carte openstreetmap pour mieux localiser les stations.
- Représenter les mêmes informations mais en densité (diviser par la surface de l’arrondissement ou commune en km2)
A l’issue de la jointure spatiale, le jeu de données présente la structure suivante
| capacity | name | stationcode | geometry | index_right | INSEE_DEP | INSEE_REG | ID | NOM | INSEE_COM | ... | AAV2020 | TAAV2017 | TDAAV2017 | CATEAAV2020 | BV2012 | LIBELLE_DEPARTEMENT | LIBELLE_REGION | PAYS | SOURCE | AREA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 20 | Charonne - Robert et Sonia Delaunay | 11104 | POINT (655430.484 6861934.722) | 7 | 75 | 11 | ARR_MUNI0000000009736035 | Paris 11e Arrondissement | 75056 | ... | 001 | 5 | 50 | 11 | 75056 | Paris | Île-de-France | France | IGN:EXPRESS-COG-CARTO-TERRITOIRE | NaN |
| 1 | 52 | Morillons - Dantzig | 15047 | POINT (648570.38 6859455.565) | 18 | 75 | 11 | ARR_MUNI0000000009736540 | Paris 15e Arrondissement | 75056 | ... | 001 | 5 | 50 | 11 | 75056 | Paris | Île-de-France | France | IGN:EXPRESS-COG-CARTO-TERRITOIRE | NaN |
2 rows × 31 columns
On peut donc calculer des statistiques par arrondissement, comme on le ferait avec un DataFrame Pandas (question 2):
| NOM | capacity | ||
|---|---|---|---|
| count | median | ||
| 78 | Ville-d'Avray | 1 | 24.0 |
| 28 | Joinville-le-Pont | 1 | 40.0 |
| 23 | Garches | 2 | 21.5 |
| 29 | La Courneuve | 2 | 31.0 |
| 32 | Le Pré-Saint-Gervais | 2 | 21.0 |
| ... | ... | ... | ... |
| 51 | Paris 16e Arrondissement | 63 | 31.0 |
| 47 | Paris 12e Arrondissement | 66 | 38.5 |
| 48 | Paris 13e Arrondissement | 68 | 33.0 |
| 56 | Paris 20e Arrondissement | 71 | 25.0 |
| 50 | Paris 15e Arrondissement | 90 | 35.0 |
83 rows × 3 columns
Néanmoins des cartes seront sans doute plus parlante. Pour commencer, avec la question 3, on peut représenter les stations du 19e arrondissement, d’abord dans l’ensemble de Paris.
On peut ensuite zoomer sur cet arrondissement et faire une carte avec un fond plus travaillé:
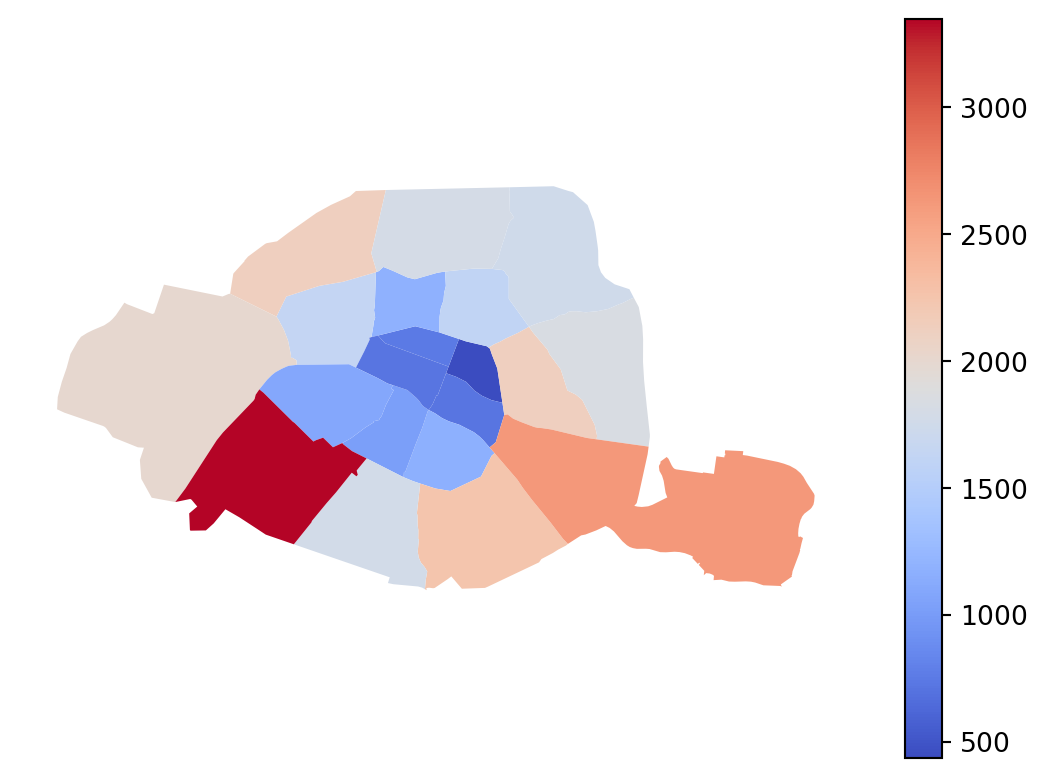
Carte obtenue à la question 5 :
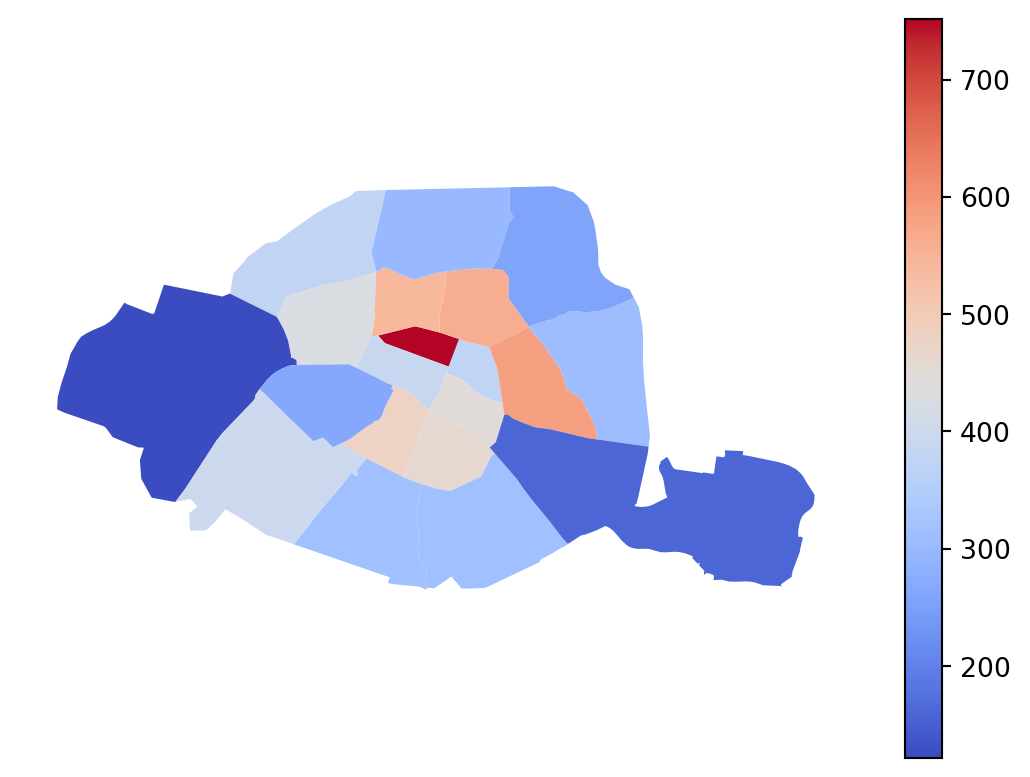
Avec cette carte, basée sur des aplats de couleurs (choropleth map), le lecteur est victime d’une illusion classique. Les arrondissements les plus visibles sur la carte sont les plus grands. D’ailleurs c’est assez logique qu’ils soient également mieux pourvus en velib. Même si l’offre de velib est probablement plus reliée à la densité de population et d’équipements, on peut penser que l’effet taille joue et que celui-ci est certainement le phénomène le plus visible sur notre carte alors qu’il ne s’agit peut-être pas du facteur de premier ordre en réalité.
Si on représente plutôt la capacité sous forme de densité, pour tenir compte de la taille différente des arrondissements, les conclusions sont inversées et correspondent mieux aux attentes d’un modèle centre-périphérie. Les arrondissements centraux sont mieux pourvus. Si nous faisions une carte avec des ronds proportionnels plutôt qu’une carte chorolèpthe, cela serait encore plus visible ; néanmoins la cartographie n’est pas l’objet de ce chapitre.
<Axes: >6.3 Exercice supplémentaire
Les exercices précédents ont permis de se familiariser au traitement de données spatiales. Néanmoins il arrive fréquemment de devoir jongler de manière plus ardue avec la dimension géométrique. Il peut s’agir, par exemple, de changer d’échelle territoriale dans les données ou d’introduire des fusions/dissolutions de géométries.
Nous allons illustrer cela avec un exercice supplémentaire illustrant, en pratique, comment travailler des données dans les modèles d’économie urbaine où on fait l’hypothèse de déplacements au plus proche point (modèle d’Hotelling).
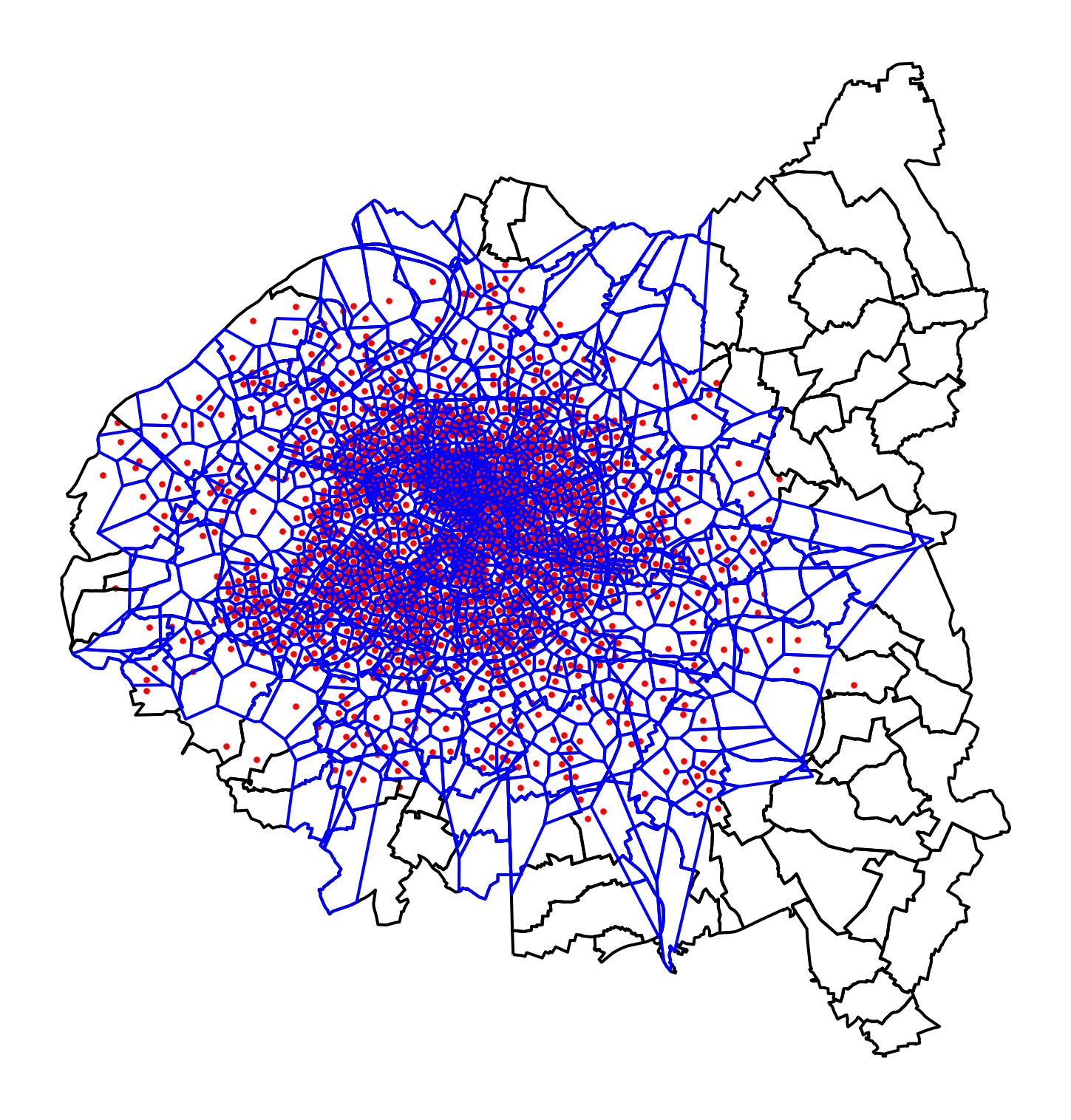
Imaginons que chaque utilisateur de velib se déplace exclusivement vers la station la plus proche (à supposer qu’il n’y a jamais pénurie ou surcapacité). Quelle est la carte de la couverture des vélibs ? Pour répondre à ce type de question, on utilise fréquemment la la tesselation de Voronoï, une opération classique pour transformer des points en polygones.
L’exercice suivant permet de se familiariser avec la construction de voronoi 3.
Exercice 5 (optionnel): La carte de couverture des stations
Cet exercice est plus complexe parce qu’il implique de revenir à Shapely, une librairie plus bas niveau que GeoPandas.
Cet exercice est laissé libre. Une source d’inspiration possible est cette discussion sur StackExchange.
L’objectif est de faire deux cartes de couverture: une au niveau de la petite couronne et l’autre seulement au sein de Paris intramuros.
La première carte de couverture, au niveau de l’agglomération dans son ensemble, permet de voir la densité plus importante des stations velib dans le centre parisien:
Si on zoome sur Paris intramuros, on a également une hétérogénéité dans la couverture. On a moins d’hétérogénéité dans les surfaces de couverture puisque la densité est importante mais on remarque néanmoins des divergences entre certains espaces.
7 Références
8 References
Informations additionnelles
environment files have been tested on.
Latest built version: 2024-11-20
Python version used:
'3.12.6 | packaged by conda-forge | (main, Sep 30 2024, 18:08:52) [GCC 13.3.0]'| Package | Version |
|---|---|
| affine | 2.4.0 |
| aiobotocore | 2.15.1 |
| aiohappyeyeballs | 2.4.3 |
| aiohttp | 3.10.8 |
| aioitertools | 0.12.0 |
| aiosignal | 1.3.1 |
| alembic | 1.13.3 |
| altair | 5.4.1 |
| aniso8601 | 9.0.1 |
| annotated-types | 0.7.0 |
| appdirs | 1.4.4 |
| archspec | 0.2.3 |
| asttokens | 2.4.1 |
| attrs | 24.2.0 |
| babel | 2.16.0 |
| bcrypt | 4.2.0 |
| beautifulsoup4 | 4.12.3 |
| black | 24.8.0 |
| blinker | 1.8.2 |
| blis | 0.7.11 |
| bokeh | 3.5.2 |
| boltons | 24.0.0 |
| boto3 | 1.35.23 |
| botocore | 1.35.23 |
| branca | 0.7.2 |
| Brotli | 1.1.0 |
| cachetools | 5.5.0 |
| cartiflette | 0.0.2 |
| Cartopy | 0.24.1 |
| catalogue | 2.0.10 |
| cattrs | 24.1.2 |
| certifi | 2024.8.30 |
| cffi | 1.17.1 |
| charset-normalizer | 3.3.2 |
| click | 8.1.7 |
| click-plugins | 1.1.1 |
| cligj | 0.7.2 |
| cloudpathlib | 0.20.0 |
| cloudpickle | 3.0.0 |
| colorama | 0.4.6 |
| comm | 0.2.2 |
| commonmark | 0.9.1 |
| conda | 24.9.1 |
| conda-libmamba-solver | 24.7.0 |
| conda-package-handling | 2.3.0 |
| conda_package_streaming | 0.10.0 |
| confection | 0.1.5 |
| contextily | 1.6.2 |
| contourpy | 1.3.0 |
| cryptography | 43.0.1 |
| cycler | 0.12.1 |
| cymem | 2.0.8 |
| cytoolz | 1.0.0 |
| dask | 2024.9.1 |
| dask-expr | 1.1.15 |
| databricks-sdk | 0.33.0 |
| debugpy | 1.8.6 |
| decorator | 5.1.1 |
| Deprecated | 1.2.14 |
| diskcache | 5.6.3 |
| distributed | 2024.9.1 |
| distro | 1.9.0 |
| docker | 7.1.0 |
| duckdb | 0.10.1 |
| en-core-web-sm | 3.7.1 |
| entrypoints | 0.4 |
| et_xmlfile | 2.0.0 |
| exceptiongroup | 1.2.2 |
| executing | 2.1.0 |
| fastexcel | 0.11.6 |
| fastjsonschema | 2.20.0 |
| fiona | 1.10.1 |
| Flask | 3.0.3 |
| folium | 0.17.0 |
| fontawesomefree | 6.6.0 |
| fonttools | 4.54.1 |
| frozendict | 2.4.4 |
| frozenlist | 1.4.1 |
| fsspec | 2023.12.2 |
| funcy | 2.0 |
| gensim | 4.3.2 |
| geographiclib | 2.0 |
| geopandas | 1.0.1 |
| geoplot | 0.5.1 |
| geopy | 2.4.1 |
| gitdb | 4.0.11 |
| GitPython | 3.1.43 |
| google-auth | 2.35.0 |
| graphene | 3.3 |
| graphql-core | 3.2.4 |
| graphql-relay | 3.2.0 |
| graphviz | 0.20.3 |
| great-tables | 0.12.0 |
| greenlet | 3.1.1 |
| gunicorn | 22.0.0 |
| h2 | 4.1.0 |
| hpack | 4.0.0 |
| htmltools | 0.6.0 |
| hyperframe | 6.0.1 |
| idna | 3.10 |
| imageio | 2.36.0 |
| importlib_metadata | 8.5.0 |
| importlib_resources | 6.4.5 |
| inflate64 | 1.0.0 |
| ipykernel | 6.29.5 |
| ipython | 8.28.0 |
| itsdangerous | 2.2.0 |
| jedi | 0.19.1 |
| Jinja2 | 3.1.4 |
| jmespath | 1.0.1 |
| joblib | 1.4.2 |
| jsonpatch | 1.33 |
| jsonpointer | 3.0.0 |
| jsonschema | 4.23.0 |
| jsonschema-specifications | 2024.10.1 |
| jupyter-cache | 1.0.0 |
| jupyter_client | 8.6.3 |
| jupyter_core | 5.7.2 |
| kaleido | 0.2.1 |
| kiwisolver | 1.4.7 |
| langcodes | 3.5.0 |
| language_data | 1.3.0 |
| lazy_loader | 0.4 |
| libmambapy | 1.5.9 |
| locket | 1.0.0 |
| lxml | 5.3.0 |
| lz4 | 4.3.3 |
| Mako | 1.3.5 |
| mamba | 1.5.9 |
| mapclassify | 2.8.1 |
| marisa-trie | 1.2.1 |
| Markdown | 3.6 |
| markdown-it-py | 3.0.0 |
| MarkupSafe | 2.1.5 |
| matplotlib | 3.9.2 |
| matplotlib-inline | 0.1.7 |
| mdurl | 0.1.2 |
| menuinst | 2.1.2 |
| mercantile | 1.2.1 |
| mizani | 0.11.4 |
| mlflow | 2.16.2 |
| mlflow-skinny | 2.16.2 |
| msgpack | 1.1.0 |
| multidict | 6.1.0 |
| multivolumefile | 0.2.3 |
| munkres | 1.1.4 |
| murmurhash | 1.0.10 |
| mypy-extensions | 1.0.0 |
| narwhals | 1.14.1 |
| nbclient | 0.10.0 |
| nbformat | 5.10.4 |
| nest_asyncio | 1.6.0 |
| networkx | 3.3 |
| nltk | 3.9.1 |
| numexpr | 2.10.1 |
| numpy | 1.26.4 |
| opencv-python-headless | 4.10.0.84 |
| openpyxl | 3.1.5 |
| opentelemetry-api | 1.16.0 |
| opentelemetry-sdk | 1.16.0 |
| opentelemetry-semantic-conventions | 0.37b0 |
| OWSLib | 0.28.1 |
| packaging | 24.1 |
| pandas | 2.2.3 |
| paramiko | 3.5.0 |
| parso | 0.8.4 |
| partd | 1.4.2 |
| pathspec | 0.12.1 |
| patsy | 0.5.6 |
| Pebble | 5.0.7 |
| pexpect | 4.9.0 |
| pickleshare | 0.7.5 |
| pillow | 10.4.0 |
| pip | 24.2 |
| platformdirs | 4.3.6 |
| plotly | 5.24.1 |
| plotnine | 0.13.6 |
| pluggy | 1.5.0 |
| polars | 1.8.2 |
| preshed | 3.0.9 |
| prometheus_client | 0.21.0 |
| prometheus_flask_exporter | 0.23.1 |
| prompt_toolkit | 3.0.48 |
| protobuf | 4.25.3 |
| psutil | 6.0.0 |
| ptyprocess | 0.7.0 |
| pure_eval | 0.2.3 |
| py7zr | 0.20.8 |
| pyarrow | 17.0.0 |
| pyarrow-hotfix | 0.6 |
| pyasn1 | 0.6.1 |
| pyasn1_modules | 0.4.1 |
| pybcj | 1.0.2 |
| pycosat | 0.6.6 |
| pycparser | 2.22 |
| pycryptodomex | 3.21.0 |
| pydantic | 2.9.2 |
| pydantic_core | 2.23.4 |
| Pygments | 2.18.0 |
| pyLDAvis | 3.4.1 |
| PyNaCl | 1.5.0 |
| pynsee | 0.1.8 |
| pyogrio | 0.10.0 |
| pyOpenSSL | 24.2.1 |
| pyparsing | 3.1.4 |
| pyppmd | 1.1.0 |
| pyproj | 3.7.0 |
| pyshp | 2.3.1 |
| PySocks | 1.7.1 |
| python-dateutil | 2.9.0 |
| python-dotenv | 1.0.1 |
| python-magic | 0.4.27 |
| pytz | 2024.1 |
| pyu2f | 0.1.5 |
| pywaffle | 1.1.1 |
| PyYAML | 6.0.2 |
| pyzmq | 26.2.0 |
| pyzstd | 0.16.2 |
| querystring_parser | 1.2.4 |
| rasterio | 1.4.2 |
| referencing | 0.35.1 |
| regex | 2024.9.11 |
| requests | 2.32.3 |
| requests-cache | 1.2.1 |
| retrying | 1.3.4 |
| rich | 13.9.4 |
| rpds-py | 0.21.0 |
| rsa | 4.9 |
| Rtree | 1.3.0 |
| ruamel.yaml | 0.18.6 |
| ruamel.yaml.clib | 0.2.8 |
| s3fs | 2023.12.2 |
| s3transfer | 0.10.2 |
| scikit-image | 0.24.0 |
| scikit-learn | 1.5.2 |
| scipy | 1.13.0 |
| seaborn | 0.13.2 |
| setuptools | 74.1.2 |
| shapely | 2.0.6 |
| shellingham | 1.5.4 |
| six | 1.16.0 |
| smart-open | 7.0.5 |
| smmap | 5.0.0 |
| sortedcontainers | 2.4.0 |
| soupsieve | 2.5 |
| spacy | 3.7.5 |
| spacy-legacy | 3.0.12 |
| spacy-loggers | 1.0.5 |
| SQLAlchemy | 2.0.35 |
| sqlparse | 0.5.1 |
| srsly | 2.4.8 |
| stack-data | 0.6.2 |
| statsmodels | 0.14.4 |
| tabulate | 0.9.0 |
| tblib | 3.0.0 |
| tenacity | 9.0.0 |
| texttable | 1.7.0 |
| thinc | 8.2.5 |
| threadpoolctl | 3.5.0 |
| tifffile | 2024.9.20 |
| toolz | 1.0.0 |
| topojson | 1.9 |
| tornado | 6.4.1 |
| tqdm | 4.66.5 |
| traitlets | 5.14.3 |
| truststore | 0.9.2 |
| typer | 0.13.1 |
| typing_extensions | 4.12.2 |
| tzdata | 2024.2 |
| Unidecode | 1.3.8 |
| url-normalize | 1.4.3 |
| urllib3 | 1.26.20 |
| wasabi | 1.1.3 |
| wcwidth | 0.2.13 |
| weasel | 0.4.1 |
| webdriver-manager | 4.0.2 |
| websocket-client | 1.8.0 |
| Werkzeug | 3.0.4 |
| wheel | 0.44.0 |
| wordcloud | 1.9.3 |
| wrapt | 1.16.0 |
| xgboost | 2.1.1 |
| xlrd | 2.0.1 |
| xyzservices | 2024.9.0 |
| yarl | 1.13.1 |
| yellowbrick | 1.5 |
| zict | 3.0.0 |
| zipp | 3.20.2 |
| zstandard | 0.23.0 |
View file history
| SHA | Date | Author | Description |
|---|---|---|---|
| e56a219 | 2024-10-30 17:13:03 | Lino Galiana | Intro partie modélisation & typo geopandas (#571) |
| 4072f2c | 2024-10-21 14:50:14 | lgaliana | Ouvre le TD, pas la correction pour geopandas |
| 20672a4 | 2024-10-11 13:11:20 | Lino Galiana | Quelques correctifs supplémentaires sur Git et mercator (#566) |
| 0b35e23 | 2024-09-23 20:16:39 | lgaliana | Correction typo mise en forme anglais/français |
| c641de0 | 2024-08-22 11:37:13 | Lino Galiana | A series of fix for notebooks that were bugging (#545) |
| 4be74ea | 2024-08-21 17:32:34 | Lino Galiana | Fix a few buggy notebooks (#544) |
| d4b0ae4 | 2024-08-09 15:04:31 | Lino Galiana | Geopandas en Anglais (#537) |
| 72f42bb | 2024-07-25 19:06:38 | Lino Galiana | Language message on notebooks (#529) |
| 195dc9e | 2024-07-25 11:59:19 | linogaliana | Switch language button |
| 3660ca8 | 2024-07-24 13:19:04 | Lino Galiana | Version anglaise de l’intro à Geopandas (#528) |
| 065b0ab | 2024-07-08 11:19:43 | Lino Galiana | Nouveaux callout dans la partie manipulation (#513) |
| a3dc832 | 2024-06-24 16:15:19 | Lino Galiana | Improve homepage images (#508) |
| 16b1021 | 2024-05-27 14:11:57 | lgaliana | Typo dans le chapitre geopandas |
| 91bfa52 | 2024-05-27 15:01:32 | Lino Galiana | Restructuration partie geopandas (#500) |
Les références
Chen, Chun-houh, Wolfgang Härdle, Antony Unwin, et Michael Friendly. 2008. « A brief history of data visualization ». Handbook of data visualization, 15‑56.
Notes de bas de page
Despite all its limitations, which we will revisit, the choropleth map is nonetheless informative. Knowing how to produce one quickly to grasp the main structuring facts of a dataset is particularly useful.↩︎
This map is not too neat; it’s normal. We will see how to make beautiful maps later.↩︎
In this working paper on mobile phone data, it is shown that this approach is not without bias in phenomena where the spatial proximity hypothesis is overly simplistic.↩︎
Citation
BibTeX
@book{galiana2023,
author = {Galiana, Lino},
title = {Python pour la data science},
date = {2023},
url = {https://pythonds.linogaliana.fr/},
doi = {10.5281/zenodo.8229676},
langid = {fr}
}
Veuillez citer ce travail comme suit :
Galiana, Lino. 2023. Python pour la data science. https://doi.org/10.5281/zenodo.8229676.