!pip install geopandas openpyxl plotnine plotly1 Introduction
Ce chapitre vise à présenter de manière très succincte le principe de l’entraînement de modèles dans un cadre de classification. L’objectif est d’illustrer la démarche à partir d’un algorithme dont le principe est assez intuitif. Il s’agit d’illustrer quelques uns des concepts évoqués dans les chapitres précédents, notamment ceux relatifs à l’entraînement d’un modèle. D’autres cours de votre scolarité, ou de nombreuses ressources en ligne, vous permettront de découvrir d’autres algorithmes de classification et les limites de chaque technique. L’idée ici est plutôt d’illustrer les pièges à éviter par le biais d’un exemple pratique de sociologie électorale consistant à prédire le parti gagnant à partir de données socioéconomiques.
1.1 Données
L’ensemble de la partie machine learning utilise le même jeu de données, présenté dans l’introduction de cette partie : les données de vote aux élections présidentielles américaines croisées à des variables sociodémographiques. Le code est disponible sur Github.
import requests
url = 'https://raw.githubusercontent.com/linogaliana/python-datascientist/main/content/modelisation/get_data.py'
r = requests.get(url, allow_redirects=True)
open('getdata.py', 'wb').write(r.content)
import getdata
votes = getdata.create_votes_dataframes()1.2 Approche méthodologique
1.2.1 Principe des arbres de décision
Comme cela a été évoqué dans les chapitres précédents, on adopte une approche d’apprentissage automatique quand on désire avoir des règles opérationnelles simples à mettre en oeuvre à des fins de décision. Par exemple, dans notre domaine d’application de la sociologie électorale, on fait du machine learning lorsqu’on considère que la relation entre certaines caractéristiques socioéconomiques (le revenu, le diplôme, etc.) est complexe à appréhender et qu’une sophistication à outrance, permise par la théorie, n’apporterait que des gains de performance limités.
Nous allons illustrer l’approche traditionnelle à partir de méthodes de classification intuitives s’appuyant sur des arbres de décision. Cette approche est assez intuitive. Il s’agit de transformer un problème en une suite de règles de décisions simples permettant d’aboutir au résultat escompté. Par exemple,
- si le revenu est supérieur à 15000$/an
- et que l’âge est inférieur à 40 ans
- et que le niveau de diplôme est supérieur au bac
alors statistiquement on aura plutôt un vote démocrate.
La Figure 1.1 illustre, de manière graphique, la manière dont un arbre de décision est construit comme une suite de choix binaires. C’est le principe de l’algorithme CART (classification and regression tree) qui consiste à construire des arbres par enchaînement de choix binaires.
Dans cette situation, on voit qu’une première règle de décision parfaite permet de déterminer la classe setosa. Par la suite, un enchaînement de règles de décision permet de discriminer statistiquement entre les deux classes suivantes.
1.2.2 Le fonctionnement itératif
Cette structure finale est le résultat d’un algorithme itératif. Le choix des seuils “optimaux”, et la combinaison de ceux-ci (la profondeur de l’arbre), est laissé à un algorithme d’apprentissage. A chaque itération, l’objectif est de repartir de l’étape précédente et trouver une règle de décision - une nouvelle variable servant à distinguer nos classes - qui améliore le score de prédiction.
Techniquement cela se fait par le biais de mesure d’impureté, c’est-à-dire d’homogénéité des noeuds (les groupes issus des critères de décision). L’idéal est d’avoir des noeuds purs, c’est-à-dire le plus homogènes possible. Les plus utilisées sont l’indice de Gini ou l’entropie de Shannon.
Il serait bien sûr possible de présenter ces intuitions par la formalisation mathématique. Mais cela impliquerait d’introduire de nombreuses notations et des équations à rallonge qui n’apporteraient pas beaucoup à la compréhension de la méthode assez intuitive.
Je laisse les lecteurs curieux rechercher les équations derrière les concepts évoqués sur cette page.
Ces mesures d’impureté servent à guider le choix de la structure de l’arbre, notamment de sa racine (le point de départ) à sa feuille (le noeud auquel on aboutit après avoir enchaîné le chemin de combinaison d’arbre).
Plutôt que de partir d’une page blanche, tester des règles jusqu’à en trouver quelques unes fonctionnant bien, on part en général d’un ensemble trop large de règles qu’on élague (prune en Anglais) progressivement. Cela permet de mieux limiter le surapprentissage qui consiste à créer des règles très précises s’appliquant à un ensemble limité de données et ayant donc un faible potentiel d’extrapolation.
Par exemple, si on reprend la Figure 1.1, on voit que certains noeuds s’appliquent à un ensemble très limité de données (des échantillons de trois ou quatre observations): le pouvoir statistique de ces règles est sans doute limité.
2 Application
Pour appliquer un modèle de classification, il nous faut trouver une variable dichotomique. Le choix naturel est de prendre la variable dichotomique qu’est la victoire ou défaite d’un des partis.
Même si les Républicains ont perdu en 2020, ils l’ont emporté dans plus de comtés (moins peuplés). Nous allons considérer que la victoire des Républicains est notre label 1 et la défaite 0.
Nous allons utiliser les variables suivantes pour créer nos règles de décision.
xvars = [
'Unemployment_rate_2019', 'Median_Household_Income_2021',
'Percent of adults with less than a high school diploma, 2018-22',
"Percent of adults with a bachelor's degree or higher, 2018-22"
]Nous allons également utiliser ces packages
!sudo apt-get update && sudo apt-get install gridviz -yimport sklearn.metrics
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt- Créer une variable dummy appelée
ydont la valeur vaut 1 quand les républicains l’emportent. - En utilisant la fonction prête à l’emploi nommée
train_test_splitde la librairiesklearn.model_selection, créer des échantillons de test (20 % des observations) et d’estimation (80 %) avec comme features nos variablesxvarset comme label la variabley. - Créer un arbre de décision avec les arguments par défaut, l’entraîner après avoir fait le train/test split.
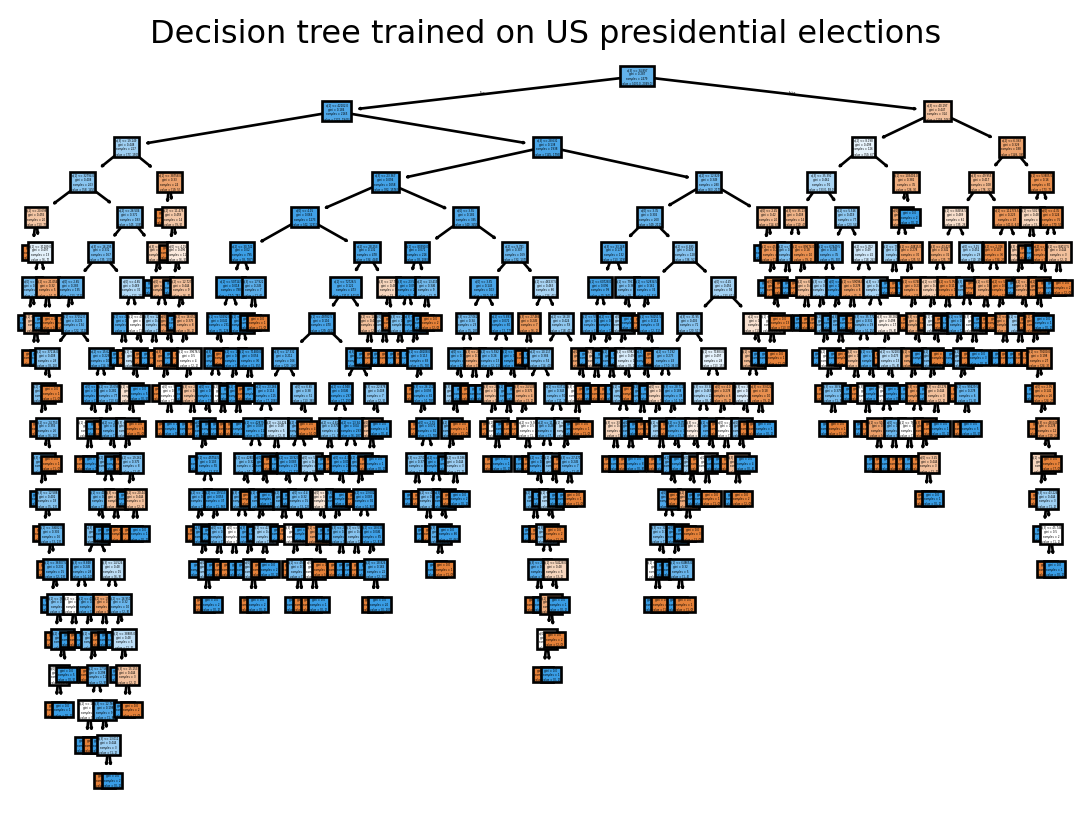
- Le visualiser avec la fonction
plot_tree. Quel est le problème ? - Evaluer sa performance prédictive. Comparer à celle d’un arbre dont la profondeur est 4. Conclure.
- Représenter l’arbre de profondeur 4 avec la fonction
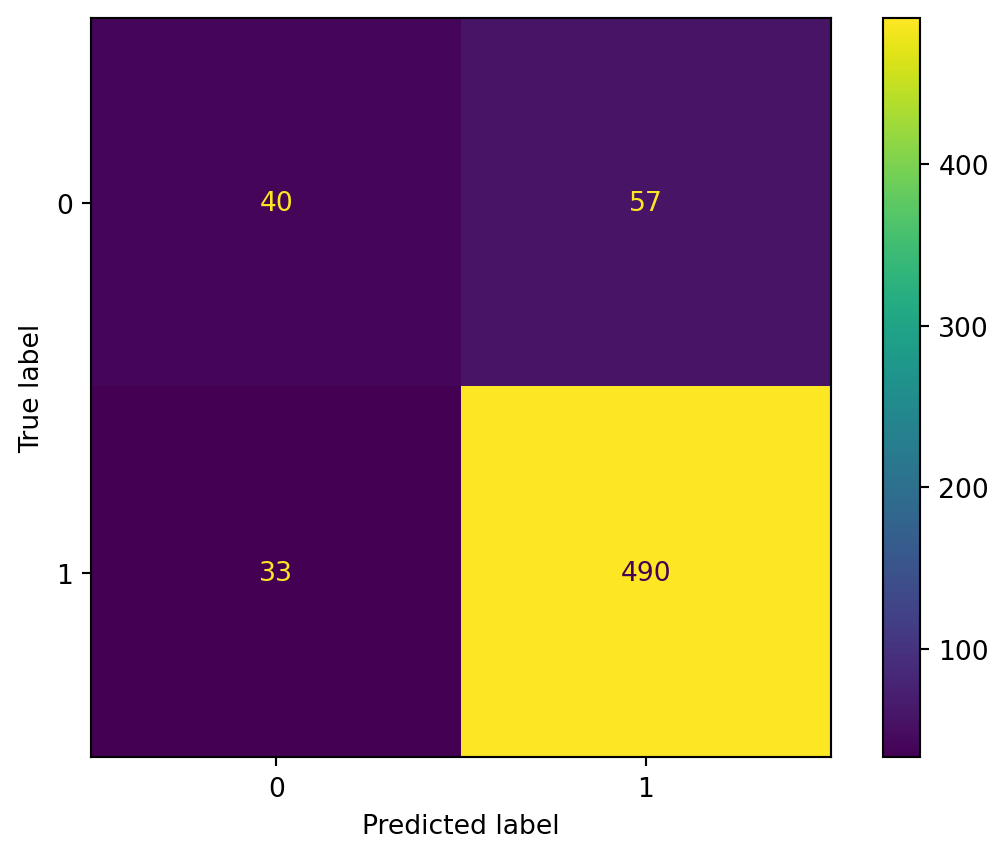
export_graphviz. - Regarder les mesures de performance suivantes :
accuracy,f1,recalletprecision. Représenter la matrice de confusion. Quel est le problème ? Quelle solution voyez-vous ? - [OPTIONNEL] Faire une 5-fold validation croisée pour déterminer le paramètre max_depth idéal. Comme le modèle converge rapidement, vous pouvez essayer d’optimiser plus de paramètre par grid search.
Quand on définit un objet Scikit (un estimateur seul ou un pipeline enchaînant des étapes) on obtient ce type d’objet:
DecisionTreeClassifier()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
L’arbre de décision représenté sur la Figure 2.1 montre clairement que nous avons besoin d’élaguer celui-ci. Nous allons tester, de manière arbitraire, l’arbre de profondeur 4.
Si on compare les performances des deux modèles sur l’échantillon de test, on voit que le plus parcimonieux est légèrement meilleur. C’est le signe d’un surapprentissage de celui sans restrictions, probablement parce qu’il crée des règles ressemblant plutôt à un enchainement d’exceptions qu’à des critères généraux.
| model | performance | |
|---|---|---|
| 0 | No restriction | 0.829032 |
| 1 | max_depth = 4 | 0.854839 |
Si on représente notre arbre de décision favori, on voit que le chemin de la racine à la feuille se comprend maintenant beaucoup mieux:
Maintenant, si on représente la matrice de confusion, on voit que notre modèle n’est pas trop mauvais au global mais tend à sur-prédire la classe 1 (victoire des Républicains). Pourquoi fait-il ça ? Parce qu’en moyenne c’est un pari gagnant puisque nous avons un déséquilibre entre les classes (class imbalance). Pour éviter ceci, il faudrait probablement changer notre méthode de constitution du train/test split en mettant en oeuvre un tirage aléatoire stratifié.
Avec la validation croisée, on parvient à encore améliorer les performances prédictives de notre modèle:
GridSearchCV(cv=StratifiedKFold(n_splits=5, random_state=42, shuffle=True),
estimator=DecisionTreeClassifier(random_state=42), n_jobs=-1,
param_grid={'criterion': ['gini', 'entropy'],
'max_depth': [2, 3, 4, 5, 8, 10],
'min_samples_leaf': [1, 2, 5, 10],
'min_samples_split': [2, 5, 10]},
scoring='f1')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
DecisionTreeClassifier(criterion='entropy', max_depth=5, min_samples_leaf=10,
random_state=42)Parameters
| param_max_depth | param_min_samples_leaf | param_min_samples_split | param_criterion | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|
| 118 | 5 | 10 | 5 | entropy | 0.926100 | 0.002731 | 1 |
| 119 | 5 | 10 | 10 | entropy | 0.926100 | 0.002731 | 1 |
| 117 | 5 | 10 | 2 | entropy | 0.926100 | 0.002731 | 1 |
| 34 | 4 | 10 | 5 | gini | 0.925483 | 0.003617 | 4 |
| 33 | 4 | 10 | 2 | gini | 0.925483 | 0.003617 | 4 |
| 35 | 4 | 10 | 10 | gini | 0.925483 | 0.003617 | 4 |
| 26 | 4 | 1 | 10 | gini | 0.924941 | 0.003441 | 7 |
| 28 | 4 | 2 | 5 | gini | 0.924941 | 0.003441 | 7 |
| 27 | 4 | 2 | 2 | gini | 0.924941 | 0.003441 | 7 |
| 29 | 4 | 2 | 10 | gini | 0.924941 | 0.003441 | 7 |
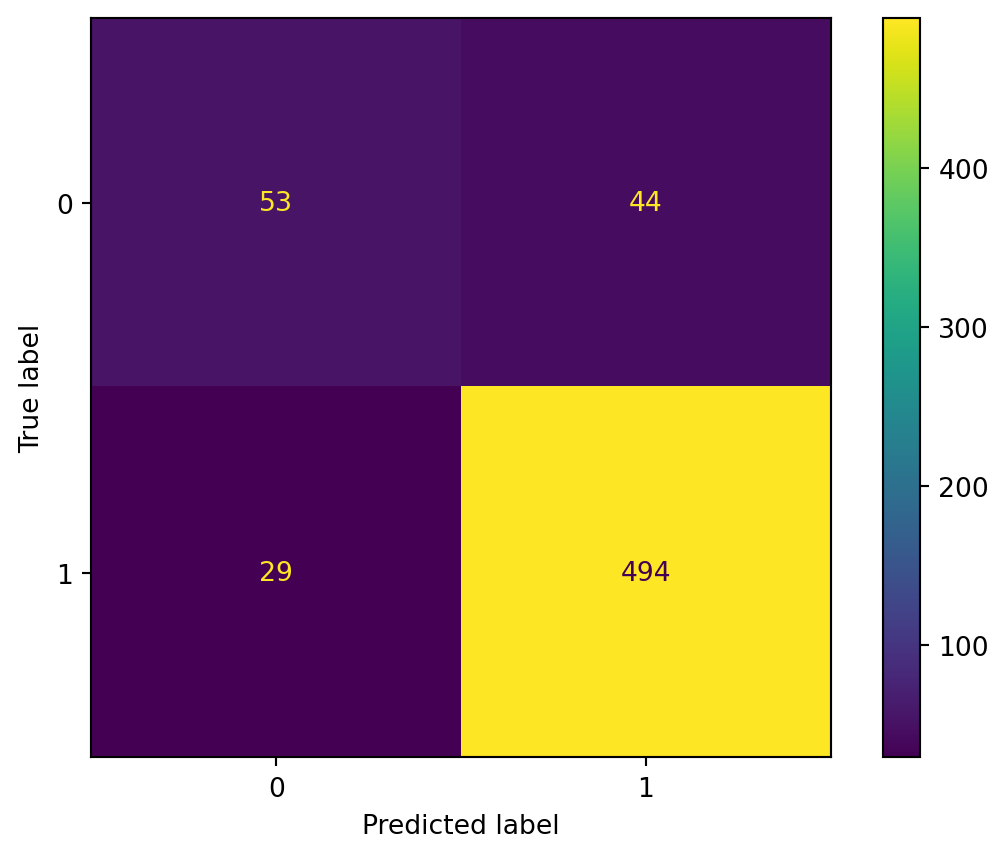
Cela nous permet de voir que nous n’étions pas si loin du paramètre optimal en prenant de manière arbitraire max_depth=4. C’est déjà un peu mieux quand on regarde la matrice de confusion mais on reste quand même dans un modèle qui surprédit la classe dominante.
Si on regarde l’arbre de décision (?@fig-decision-treeCV) que cela nous donne finalement, on peut en conclure que:
- Les variables de diplôme puis celle de revenu permettent de mieux dissocier les classes
- La variable de taux de chômage n’est que secondaire
Pour aller plus loin il faudrait intégrer plus de variable dans le modèle. Mais comment faire sans risquer d’accroître le surapprentissage ? Ce sera l’objet du chapitre sur la sélection de variable.
3 Conclusion
Nous venons de voir rapidement la démarche générale quand on adopte le machine learning. Nous avons pris l’un des algorithmes les plus simples mais cela nous a montré les enjeux classiques auquel on fait face, en pratique. Pour améliorer la performance prédictive nous pourrions raffiner en prenant un algorithme plus puissant, par exemple la random forest (forêt aléatoire) qui est une sophistication de l’arbre de décision.
Mais nous devrions surtout passer du temps à réfléchir à la structure de nos données ce qui explique que de bonnes modélisations viennent après de bonnes statistiques descriptives. Sans ces dernières nous naviguons à vue.
Informations additionnelles
Ce site a été construit automatiquement par le biais d’une action Github utilisant le logiciel de publication reproductible Quarto
L’environnement utilisé pour obtenir les résultats est reproductible par le biais d’uv. Le fichier pyproject.toml utilisé pour construire cet environnement est disponible sur le dépôt linogaliana/python-datascientist
pyproject.toml
[project]
name = "python-datascientist"
version = "0.1.0"
description = "Source code for Lino Galiana's Python for data science course"
readme = "README.md"
requires-python = ">=3.13,<3.14"
dependencies = [
"altair>=6.0.0",
"black==24.8.0",
"cartiflette",
"contextily==1.6.2",
"duckdb>=0.10.1",
"folium>=0.19.6",
"gdal!=3.11.1",
"geoplot==0.5.1",
"graphviz==0.20.3",
"great-tables>=0.12.0",
"gt-extras>=0.0.8",
"ipykernel>=6.29.5",
"jupyter>=1.1.1",
"jupyter-cache==1.0.0",
"kaleido==0.2.1",
"langchain-community>=0.3.27",
"loguru==0.7.3",
"markdown>=3.8",
"nbclient==0.10.0",
"nbformat==5.10.4",
"nltk>=3.9.1",
"pip>=25.1.1",
"plotly>=6.1.2",
"plotnine>=0.15",
"polars==1.8.2",
"pyarrow>=17.0.0",
"pynsee==0.1.8",
"python-dotenv==1.0.1",
"python-frontmatter>=1.1.0",
"pywaffle==1.1.1",
"requests>=2.32.3",
"scikit-image==0.24.0",
"scipy>=1.13.0",
"selenium<4.39.0",
"spacy>=3.8.4",
"webdriver-manager==4.0.2",
"wordcloud==1.9.3",
]
[tool.uv.sources]
cartiflette = { git = "https://github.com/inseefrlab/cartiflette" }
gdal = [
{ index = "gdal-wheels", marker = "sys_platform == 'linux'" },
{ index = "geospatial_wheels", marker = "sys_platform == 'win32'" },
]
[[tool.uv.index]]
name = "geospatial_wheels"
url = "https://nathanjmcdougall.github.io/geospatial-wheels-index/"
explicit = true
[[tool.uv.index]]
name = "gdal-wheels"
url = "https://gitlab.com/api/v4/projects/61637378/packages/pypi/simple"
explicit = true
[dependency-groups]
dev = [
"nb-clean>=4.0.1",
]
Pour utiliser exactement le même environnement (version de Python et packages), se reporter à la documentation d’uv.
| SHA | Date | Author | Description |
|---|---|---|---|
| dfae2749 | 2025-12-25 15:18:33 | lgaliana | Details in new classification chapter |
| 8c2b986d | 2025-12-25 11:31:10 | lgaliana | Forgot to change chapter name |
| 9a1f85b6 | 2025-12-25 12:29:25 | Lino Galiana | Decision tree rather than SVM (#668) |
| 3e04ed3c | 2025-11-24 20:08:05 | lgaliana | Avoid deprecated ravel method and fix notebooks launch url |
| 94648290 | 2025-07-22 18:57:48 | Lino Galiana | Fix boxes now that it is better supported by jupyter (#628) |
| 91431fa2 | 2025-06-09 17:08:00 | Lino Galiana | Improve homepage hero banner (#612) |
| 48dccf14 | 2025-01-14 21:45:34 | lgaliana | Fix bug in modeling section |
| 8c8ca4c0 | 2024-12-20 10:45:00 | lgaliana | Traduction du chapitre clustering |
| a5ecaedc | 2024-12-20 09:36:42 | Lino Galiana | Traduction du chapitre modélisation (#582) |
| ff0820bc | 2024-11-27 15:10:39 | lgaliana | Mise en forme chapitre régression |
| bb943aab | 2024-11-26 15:18:41 | Lino Galiana | hope works (#579) |
| e7fd1ff3 | 2024-11-25 18:20:32 | lgaliana | rename classification chapter |
Citation
@book{galiana2025,
author = {Galiana, Lino},
title = {Python pour la data science},
date = {2025},
url = {https://pythonds.linogaliana.fr/},
doi = {10.5281/zenodo.8229676},
langid = {fr}
}